ট্রাপিজিয়াম কাকে বলে

ট্রাপিজিয়াম কাকে বলে ও বৈশিষ্ট্য

যে চতুর্ভুজের একজোড়া বাহু সমান্তরাল তাকে ট্রাপিজিয়াম বলে। ট্রাপিজিয়াম হলো চতুর্ভুজের একটি বিশেষ রূপ।ভাষা ও ভৌগলিক অবস্থানের ভিত্তিতে ট্রাপিজিয়াম ও ট্রাপিজয়িড সম্পর্কে সারা দুনিয়ায় পরস্পরবিরোধী একটি ধারণা প্রচলিত আছে। ট্রাপিজিয়াম শেখার শুরুতে সে বিষয়টি সম্পর্কে পরিস্কার ধারণা থাকা জরুরী।

• ট্রাপিজিয়ামের কর্ণদ্বয় তাদের ছেদবিন্দুতে একই অনুপাতে বিভক্ত হয়।
• ট্রাপিজিয়ামের তির্যক বাহুদ্বয়ের মধ্যবিন্দুর সংযোজক রেখাংশ সমান্তরাল বাহুদ্বয়ের সমান্তরাল।
• বৃত্তস্থ ট্রাপিজিয়ামের তির্যক বাহুদ্বয় পরস্পর সমান।
• ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের একটিকে ভূমি এবং অসমান্তরাল বাহুদ্বয়কে তির্যক বাহু বলা হয়।
• ট্রাপিজিয়ামের তির্যক বাহুদ্বয় সমান হলে একে সমদ্বিবাহু ট্রাপিজিয়াম বলা হয়।
• ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয় কখনো সমান হতে পারে না ।
• ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয় সমান হলে তা একটি আয়তক্ষেত্র বা বর্গক্ষেত্রে পরিণত হবে।
• ট্রাপিজিয়ামের দুইটি বাহু সমান্তরাল।
• তির্যক বাহু সংলগ্ন কোণ দুটির সমষ্টি দুই সমকোণ বা ১৮০° ।

ট্রাপিজিয়াম এর চিত্র

চতুর্ভুজের একজোড়া বিপরীত বাহু সমান্তরাল হলে তাকে ট্রাপিজিয়াম বলে।

ট্রাপিজিয়াম

ট্রাপিজিয়ামের তির্যক বাহু, সমান্তরাল বাহু, কর্ণ, ক্ষেত্রফল, ট্রাপিজিয়ামের দ্বিমধ্যমা (bimedian)ইত্যাদির উপর ভিত্তি করে ট্রাপিজিয়াম এর বৈশিষ্ট্য পরিলক্ষিত হয়। আবার, ট্রাপিজিয়ামের সন্নিহিত বাহু, সন্নিহিত কোণ, পরিসীমা ইত্যাদি বিশ্লেষণ করলেও ট্রাপিজিয়াম এর বৈশিষ্ট্য লক্ষ্য করা যায়। নিচে ট্রাপিজিয়ামের বৈশিষ্ট্য সমূহকে একত্রে উল্লেখ করা হলো:

1. ট্রাপিজিয়ামের একজোড়া বাহু পরস্পর সমান্তরাল।
2. ট্রাপিজিয়ামের অসমান্তরাল বাহু সংলগ্ন কোণ দুইটি পরস্পর সম্পূরক বা ১৮০^০।
3. ট্রাপিজিয়ামের একজোড়া বিপরীত বাহুর মধ্যবিন্দু দুইটি এবং এর কর্ণদ্বয়ের ছেদবিন্দু একই রেখায় অবস্থিত।
4. সমদ্বিবাহু ট্রাপিজিয়ামের তির্যক বাহুদ্বয় পরস্পর সমান।
5. ট্রাপিজিয়ামের একটি বাহু ও কর্ণের অন্তর্ভূক্ত কোণ ঐ বাহুর বিপরীত বাহু ও একই কর্ণের অন্তর্ভূক্ত কোণ দুইটি পরস্পর সমান।
6. ABCD একটি ট্রাপিজিয়াম হলে sinA sinC = sinB sinD সম্পর্কটি সবসময়ই সত্য হয়।
7. ট্রাপিজিয়ামের কর্ণ দুইটি পরস্পরকে একই অনুপাতে বিভক্ত করে।
8. বৃত্তে অন্তর্লিখিত কোনো ট্রাপিজিয়ামের বিপরীত কোণদ্বয়ের সমষ্টি দুই সমকোণ বা ১৮০°।
9. ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের সমষ্টিকে এর উচ্চতা দ্বারা গুণ করে প্রাপ্ত গুণফলকে অর্ধেক করলে ট্রাপিজিয়াম ক্ষেত্রের ক্ষেত্রফল পাওয়া যায়।
10. ট্রাপিজিয়ামের সমান্তরাল বিপরীত বাহু দুইটির মধ্যবর্তী দুরত্বই এর উচ্চতা বলে বিবেচিত হয়।
11. ABCD ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয় AB = a ও CD = b; অপর বাহুদ্বয় BC = c ও DA = d এবং কর্ণদ্বয় AC = e ও BD = f হলে e² + f² = c² + d² + 2ab সম্পর্কটি সবসময়ই সত্য হয়।
12. ট্রাপিজিয়ামের কর্ণদ্বয় দ্বারা ট্রাপিজিয়ামটি যে চারটি ত্রিভুজে বা বিষমবাহু ত্রিভুজ -এ বিভক্ত হয়, তাদের মধ্যে একজোড়া বিপরীত ত্রিভুজ পরস্পর সদৃশ।
13. সমান্তরাল বাহু ব্যতীত অপর দুইটি বাহুকে ট্রাপিজিয়ামের পা (legs) বলে।
14. ট্রাপিজিয়ামের কর্ণ দুইটি ট্রাপিজিয়ামটিকে যে চারটি ত্রিভুজে বিভক্ত হয়, তাদের মধ্যে একজোড়া বিপরীত ত্রিভুজের ক্ষেত্রফল পরস্পর সমান।
15. ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য ও উচ্চতা জানা থাকলে ট্রাপিজিয়াম ক্ষেত্রফল নির্ণয় করা যায়।
16. ABCD ট্রাপিজিয়ামের একজোড়া সন্নিহিত কোণের কোসাইন (cosine) এর সমষ্টি শুণ্য অর্থাৎ, cosA + cosB = 0. কারণ cosA + cosB = cosA + cos(১৮০°-A) = cosA – cosA = 0. ফলে অপর দুইটি সন্নিহিত কোণের কোসাইন (cosine) এর সমষ্টিও শুণ্য অর্থাৎ, cosC + cosD = 0.
17. ট্রাপিজিয়ামের কর্ণ দুইটি পরস্পরকে যে অনুপাতে বিভক্ত করে সেই অনুপাতটি, সমান্তরাল বাহুদ্বয়ের অনুপাতের সমান।
18. বৃত্তে অন্তর্লিখিত কোন ট্রাপিজিয়ামের কর্ণদ্বয় দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল, ঐ ট্রাপিজিয়ামের বিপরীত বাহুদ্বয় দ্বারা গঠিত দুইটি আয়তক্ষেত্রের ক্ষেত্রফলদ্বয়ের সমষ্টির সমান।
19. ট্রাপিজিয়ামের কর্ণদ্বয় দ্বারা ট্রাপিজিয়ামটি যে চারটি ত্রিভুজে বিভক্ত হয়, তাদের মধ্যে একজোড়া বিপরীত ত্রিভুজের ক্ষেত্রফল যদি X বর্গ একক ও Y বর্গ একক এবং ট্রাপিজিয়ামটির ক্ষেত্রফল A বর্গ একক হয়, তাহলে √A = √X + √Y.
20. ট্রাপিজিয়ামের বিপরীত বাহুদ্বয়ের মধ্যবিন্দু দুইটির সংযোজক রেখাংশকে দ্বিমধ্যমা (bimedian) বলে।
21. ট্রাপিজিয়ামের একটি দ্বিমধ্যমা (bimedian) ট্রাপিজিয়ামটিকে দুইটি সমান ক্ষেত্রফলবিশিষ্ট চতুর্ভুজ এ বিভক্ত করে।
22. ট্রাপিজিয়ামের তির্যক বাহুদ্বয়ের মধ্যবিন্দুর সংযোজক রেখাংশ এর সমান্তরাল বাহুদ্বয়ের সমান্তরাল।
23. ABCD ট্রাপিজিয়ামের একজোড়া সন্নিহিত কোণের কোটেন্জেন্ট (cotangent) এর সমষ্টি শুণ্য অর্থাৎ, cotA + cotB = 0. কারণ cotA + cotB = cotA + cot(180°-A) = cotA – cotA = 0. ফলে অপর দুইটি সন্নিহিত কোণের কোটেন্জেন্ট (cotangent) এর সমষ্টিও শুণ্য অর্থাৎ, cotC + cotD = 0.
24. ট্রাপিজিয়ামের তির্যক বাহুদ্বয়ের মধ্যবিন্দুদ্বয়ের সংযোজক রেখাংশের দৈর্ঘ্য এর সমান্তরাল বাহুদ্বয়ের সমষ্টির অর্ধেক।
25. ট্রাপিজিয়ামের একটি কর্ণ দ্বারা ট্রাপিজিয়ামটি যে দুইটি ত্রিভুজে বিভক্ত হয় তাদের ক্ষেত্রফলের গুণফল, অপর কর্ণ দ্বারা গঠিত ত্রিভুজ দুইটির ক্ষেত্রফলের গুণফলের সমান।
26. ট্রাপিজিয়ামের দুইটি বাহু পরস্পর সমান হলে তখন এটি সমদ্বিবাহু ট্রাপিজিয়াম হয়ে যায়।
27. ট্রাপিজিয়ামের বাহুগুলোর মধ্যবিন্দু চারটি যোগ করলে যে চতুর্ভুজটি উৎপন্ন হয় তা একটি সামান্তরিক।
28. ট্রাপিজিয়ামের কর্ণদ্বয়ের মধ্যবিন্দুর সংযোজক সরলরেখা এর সমান্তরাল বাহুদ্বয়ের সমান্তরাল।
29. সমদ্বিবাহু ট্রাপিজিয়ামের কর্ণদ্বয় পরস্পর সমান।
30. ট্রাপিজিয়ামের কর্ণদ্বয়ের মধ্যবিন্দুর সংযোজক রেখাংশের দৈর্ঘ্য, এর সমান্তরাল বাহুদ্বয়ের বিয়োগফলের অর্ধেক।
31. ট্রাপিজিয়ামের সন্নিহিত কোণ দুইটির প্রত্যেকটি সমকোণ বা ৯০° হলে, তখন এটি সমকোণী ট্রাপিজিয়াম (right trapezium) হয়ে যায়।
32. কোন ট্রাপিজিয়ামের বিপরীত কোণ দুইটি পরস্পর সম্পূরক হলে তার শীর্ষ বিন্দু চারটি সমবৃত্ত হয়। অর্থাৎ শীর্ষ বিন্দু চারটি দিয়ে অতিক্রান্ত একটি অনন্য বৃত্ত অঙ্কন করা যায়।
33. ট্রাপিজিয়ামের বৃহত্তম ভূমি-বাহু সংলগ্ন কোণ দুইটির প্রত্যেকটি সূক্ষ্মকোণ হলে তখন এটি সূক্ষ্মকোণী ট্রাপিজিয়াম হয়ে যায়।
34. ট্রাপিজিয়ামের বৃহত্তম ভূমি-বাহু সংলগ্ন কোণ দুইটির একটি সূক্ষ্মকোণ এবং একটি স্থুলকোণ হলে তখন এটি স্থুলকোণী ট্রাপিজিয়াম হয়ে যায়।
35. ট্রাপিজিয়ামের সমান্তরাল বাহু দুইটি জানা থাকলে এর কর্ণদ্বয়ের মধ্যবিন্দুর সংযোজক রেখাংশের দৈর্ঘ্য নির্ণয় করা যায়।
36. বৃত্তে অন্তর্লিখিত কোন ট্রাপিজিয়ামের কর্ণ দুইটি যদি পরস্পর লম্ব হয়, তবে তাদের ছেদ বিন্দু হতে কোন বাহুর উপর অঙ্কিত লম্ব বিপরীত বাহুকে সমদ্বিখণ্ডিত করে।

ট্রাপিজিয়াম এর বৈশিষ্ট্য

ট্রাপিজিয়ামের কয়েকটি বৈশিষ্ট্য নিচে উল্লেখ করা হলো:

1. ট্রাপিজিয়ামের দুইটি বাহু পরস্পর সমান্তরাল।
2. ট্রাপিজিয়ামের অসমান্তরাল দুইটির মধ্যবিন্দুদ্বয়ের সংযোজক সরলরেখা এর সমান্তরাল বাহুদ্বয়ের সমান্তরাল।
3. কোনো ট্রাপিজিয়ামের দুইটি বাহু পরস্পর সমান হলে তখন এটি সমদ্বিবাহু ট্রাপিজিয়াম হয়ে যায়।
4. ট্রাপিজিয়ামের তির্যক বাহু সংলগ্ন কোণ দুইটি পরস্পর সম্পূরক বা ১৮০^০।
5. ট্রাপিজিয়ামের যেকোনো একটি কর্ণ অপর কর্ণকে একই অনুপাতে বিভক্ত করে।
6. সমদ্বিবাহু ট্রাপিজিয়ামের কর্ণ দুইটির দৈর্ঘ্য পরস্পর সমান।

ট্রাপিজিয়ামের প্রকার

ট্রাপিজিয়ামের ৩ প্রকার । নিম্নে এ সম্পর্কে আলোচনা করা হলে:

1. সমদ্বিবাহু ট্রাপিজিয়াম
2. বিষম ট্রাপিজিয়াম
3. সমকোণী ট্রাপিজিয়াম

সমদ্বিবাহু ট্রাপিজিয়াম

যে ট্রাপিজিয়ামের অসমান্তরাল বাহুদুটি যদি পরস্পরের সমান হয় তাকে সমদ্বিবাহু ট্রাপিজিয়াম বলে।

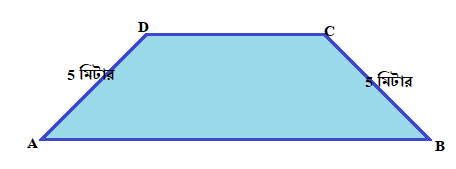
ওপরের ছবিতে দেখতে পাচ্ছেন, AD এবং BC পরস্পর অসমান্তরাল বাহুদুটি সমান। তাই ওপরের ছবিটি সমদ্বিবাহু ট্রাপিজিয়াম।

বিষম ট্রাপিজিয়াম

ট্রাপিজিয়ামের বাহু এবং কোণের পরিমাপ আলাদা বিষমবাহু ট্র্যাপিজিয়াম বলে।

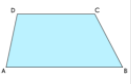
ওপরের ছবিতে দেখতে পাচ্ছেন, অসমান্তরাল বাহুদুটি পরস্পরের অসমান।

সমকোণী ট্রাপিজিয়াম

যে ট্রাপিজিয়ামের কমপক্ষে দুটি সমকোণ রয়েছে, ওই ট্রাপিজিয়ামকে সমকোণী ট্রাপিজিয়াম।

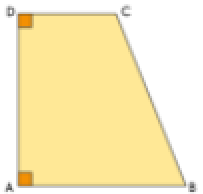
ওপরের চিত্রে দেখতে A এবং D দুটি কোণ সমকোণ।

সমদ্বিবাহু ট্রাপিজিয়াম কাকে বলে

যে ট্রাপিজিয়ামের একজোড়া বিপরীত বাহু পরস্পর সমান তাকে সমদ্বিবাহু ট্রাপিজিয়াম বলে।

সমদ্বিবাহু ট্রাপিজিয়াম হলো ট্রাপিজিয়ামের একটি বিশেষ রূপ।

অন্যভাবে বলা যায়, ট্রাপিজিয়ামের দুইটি কর্ণ সমান হলে তাকে সমদ্বিবাহু ট্রাপিজিয়াম বলে।

ট্রাপিজিয়ামের সমান্তরাল বাহু দুইটিকে ট্রাপিজিয়ামের ভূমি বলে।

একজোড়া সমান্তরাল বাহু ছাড়া অপর দুইটি বাহুকে সমদ্বিবাহু ট্রাপিজিয়ামের পা (legs) বলে।

সমদ্বিবাহু ট্রাপিজিয়ামের পা দুইটি সবসময়ই সমান।

আবার, সমদ্বিবাহু ট্রাপিজিয়ামের পা দুইটি ভূমির সাথে যে কোণ উৎপন্ন করে তাকে ভূমি কোণ (base angles) বলে। ভূমি কোণ দুইটি পরস্পর সমান।

ট্রাপিজিয়ামের সূত্র

ট্র্যাপিজয়েড নিয়ম হল এমন একটি নিয়ম যা আয়তক্ষেত্র ব্যবহার না করে মোট ক্ষেত্রফলকে ছোট ট্র্যাপিজয়েডগুলিতে ভাগ করে বক্ররেখার নীচের ক্ষেত্রফলকে মূল্যায়ন করে। এই ইন্টিগ্রেশন একটি ট্র্যাপিজয়েড হিসাবে একটি ফাংশনের গ্রাফের নীচে অঞ্চলটিকে আনুমানিক করে কাজ করে এবং এটি এলাকাটি গণনা করে।

ট্রাপিজিয়ামের ক্ষেত্রফলঃ 1/2× উচ্চতা × সমান্তরাল বাহুদ্বয়ের সমষ্টি অর্থাৎ 1/2×h×(a+b)

ট্রাপিজিয়ামের ক্ষেত্রফল

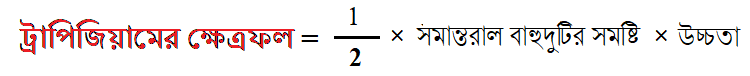
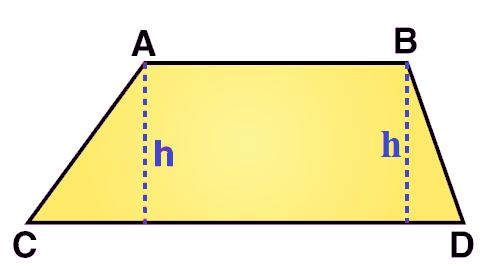
• ওপরের ছবিতে, AB এবং CD হলো দুটি সমান্তরাল বাহু।
• h হলো উচ্চতা।

ট্রাপিজিয়ামের ক্ষেত্রফল নির্ণয়ের সূত্র, ট্রাপিজিয়াম এর ক্ষেত্রফল সূত্র

ট্রাপিজিয়ামের ক্ষেত্রফল = ১/২ X (সমান্তরাল বাহুদ্বয়ের যোগফল X সমান্তরাল বাহুদ্বয়ের মধ্যবর্তী লম্ব দূরত্ব)

ট্রাপিজিয়ামের সামান্তরিক ও বৃত্ত

সামান্তরিক

চারটি বাহু থাকে এবং বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল।

চারটি কোণ থাকে এবং বিপরীত কোণগুলো পরস্পর সমান; কিন্তু কোনো কোণই সমকোণ নয়।

ট্রাপিজিয়ামের পরিসীমা নির্ণয়ের সূত্র

পরিসীমা হল যে কোনো বদ্ধ চিত্রের বাহুর সমষ্টি। অর্থাৎ , একটি ট্রাপিজিয়ামের পরিসীমা চারটি বাহুর যোগফল করলে পাওয়া যাবে।

পরিসীমা (P) = a + b + c + d

যেখানে , a, b, c, এবং d হল একটি ট্রাপিজিয়ামের বাহু।

ট্রাপিজিয়ামের বাহুগুলো অসমান। ট্রাপিজিয়ামের পরিসীমা নির্ণয়ের সাধারণ কোনো নিয়ম/সূত্র নেই। ৪ টি বাহুর সমষ্টিই ট্রাপিজিয়ামের পরিসীম অর্থাৎ,

ট্রাপিজিয়ামের পরিসীমা = ১ম বাহু + ২য় বাহু + ৩য় বাহু + ৪র্থ বাহু

আরো অন্যান্য অতি জনপ্রিয় প্রশ্নোত্তর সম্পর্কে জানার জন্য এখানে ক্লিক করুন 

FAQ | ট্রাপিজিয়াম

আপনি কি চাকরি খুজঁছেন, নিয়মিত সরকারি ও বেসরকারি চাকরির সংবাদ পেতে ক্লিক করুন। বিভিন্ন সরকারি ও বেসরকারি ক্ষেত্রে মানব সম্পদ উন্নয়ন সংক্রান্ত প্রতিবেদন পাড়ার জন্য, ক্লিক করুন। হিন্দিতে শিক্ষামূলক ব্লগ পড়তে, এখানে ক্লিক করুন। এছাড়াও, স্বাস্থ, টেকনোলজি, বিসনেস নিউস, অর্থনীতি ও আরো অন্যান্য খবর জানার জন্য, ক্লিক করুন।