মূলদ সংখ্যা কাকে বলে উদাহরণ দাও
যে সকল সংখ্যাকে ভগ্নাংশ আকারে প্রকাশ করা যায় তাই মূলদ সংখ্যা। অন্যভাবে বলা যায় , যে সকল সংখ্যাকে p/q আকারে প্রকাশ করা যায়, সে সকল সংখ্যাকে মূলদ সংখ্যা বলা হয়। যেখানে p এবং q উভয়ই পূর্ণসংখ্যা এবং q শূন্য (0) নয় এমন সংখ্যা।
আরো সহজ ভাবে বললে এভাবে বলা যায়, মূলদ সংখ্যা হলো সকল সসীম দশমিক এবং আবৃত দশমিক ভগ্নাংশ সংখ্যা।
মূলদ সংখ্যা উদাহরণ
- ৪৫ ( যে কোন পৃর্ণ সংখ্যা )
- ৩/৫ ( ভগ্নাংশ সংখ্যা )
- ৫/১০ বা ০.৫ ( সসীম দশমিক ভগ্নাংশ সংখ্যা )
- ১.৩৩৩৩৩……. ( আবৃত দশমিক ভগ্নাংশ সংখ্যা )
উদাহরণ 1: 3/5
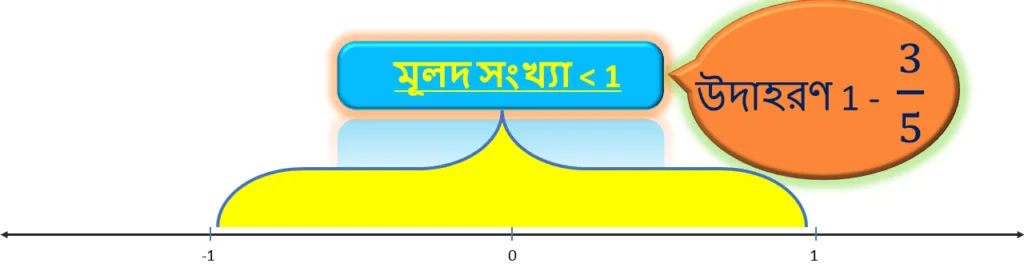
প্রথমেই আমরা দেখতে পাচ্ছি মূলদ সংখ্যাটি 1 এর থেকে ছোটো । সুতরাং , এই সংখ্যা সংখ্যারেখায় ” 0 ” থেকে ” 1 ” এর মধ্যে থাকবে
STEP – 1
| সংখ্যা | লব | হর |
| 3/5 | 3 | 5 |
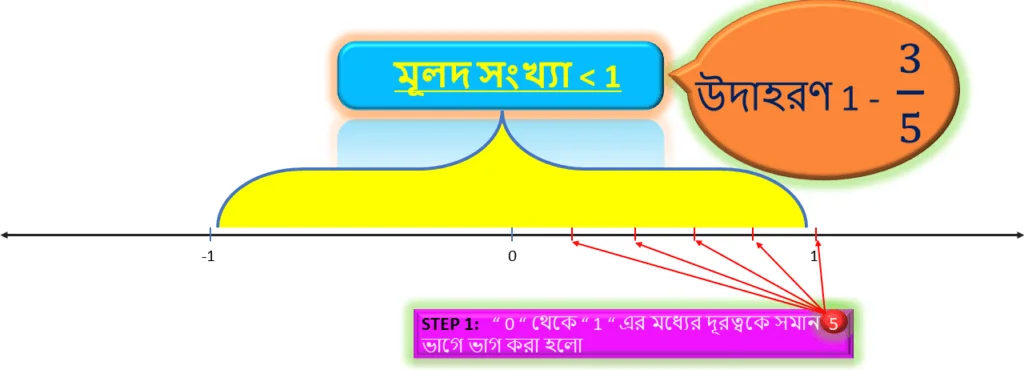
যেহেতু সংখ্যাটিতে হর = 5 , সেহেতু সংখ্যারেখায় ” 0 ” থেকে ” 1 ” এর মধ্যের দূরত্বকে সমান ” 5 ” ভাগে ভাগ করে উল্লিখিত ভাগ গুলি দাগ দ্বারা চিহ্নিত করতে হবে।
STEP – 2
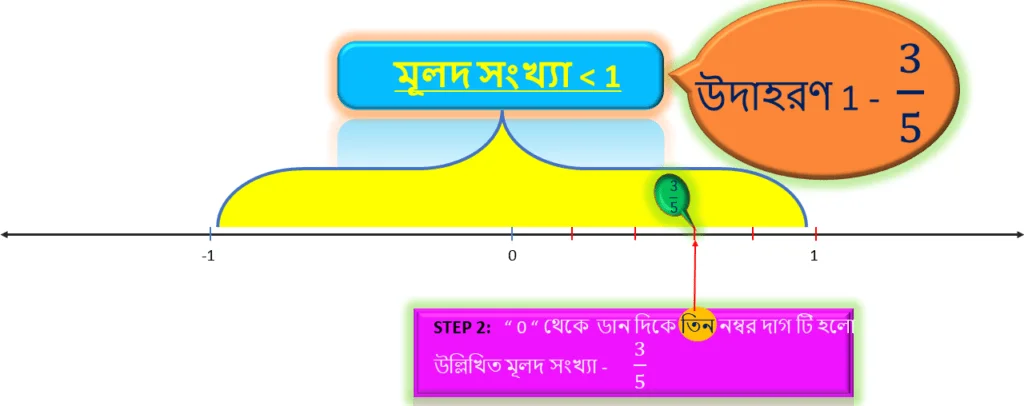
এরপর সংখ্যাটিতে দেখতে পাচ্ছি লব = 3 , অতএব এর আগে যে আমরা ” 0 ” থেকে ” 1 ” এর মধ্যের দূরত্বকে সমান ” 5 ” ভাগে ভাগ করেছি তার মধ্যে ” 0 ” থেকে ডান দিকে তিন নাম্বার দাগ টি হবে উল্লিখিত মূলদ সংখ্যা 3/5 .
উদাহরণ 2: -3/5
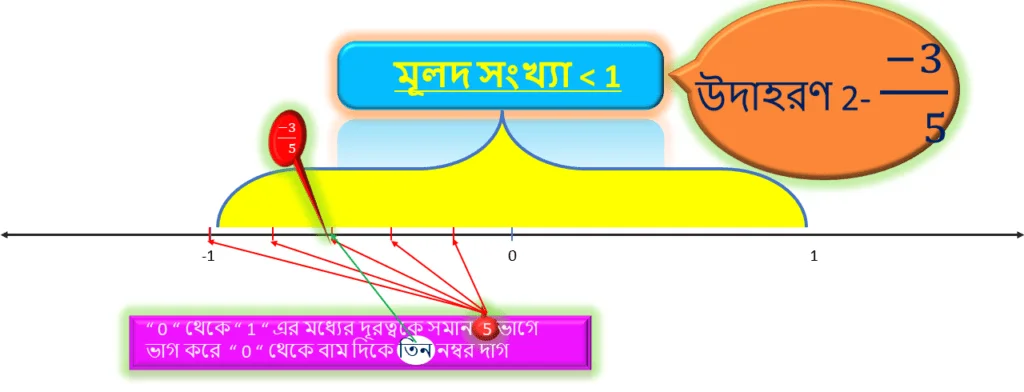
এই উদাহরণ টি আগের মতোই হবে। এর আগের উদাহরণে আমরা ” 0 ” থেকে ডান দিকে বসিয়েছি , এই উদাহরণে একই ভাবে করতে হবে শুধু এটা ” 0 ” থেকে বাম দিকে বসবে।
উদাহরণ 3: – 7/9
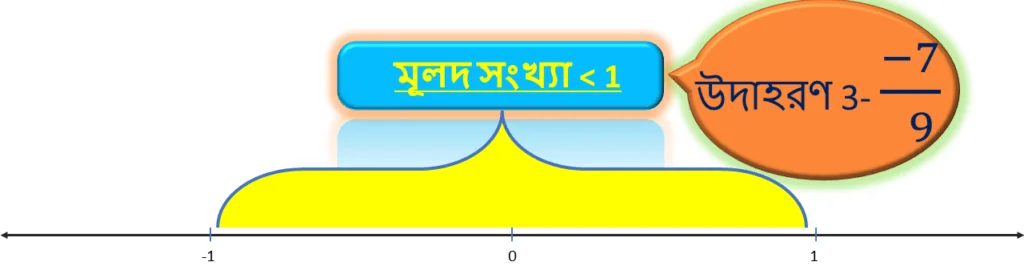
প্রথমেই আমরা দেখতে পাচ্ছি মূলদ সংখ্যাটি -1 এর থেকে বড়ো এবং ঋনাত্বক । সুতরাং , এই সংখ্যা সংখ্যারেখায় ” 0 ” থেকে ” – 1 ” এর মধ্যে থাকবে ।
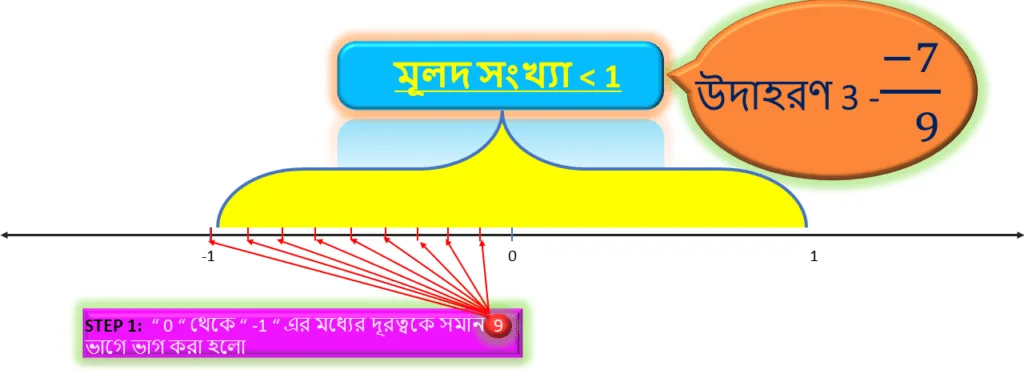
STEP -1
| সংখ্যা | লব | হর |
| – 7/9 | 7 | 9 |
যেহেতু সংখ্যাটিতে হর = 9 , সেহেতু সংখ্যারেখায় ” 0 ” থেকে ” -1 ” এর মধ্যের দূরত্বকে সমান ” 9 ” ভাগে ভাগ করে উল্লিখিত ভাগ গুলি দাগ দ্বারা চিহ্নিত করতে হবে।
STEP – 2
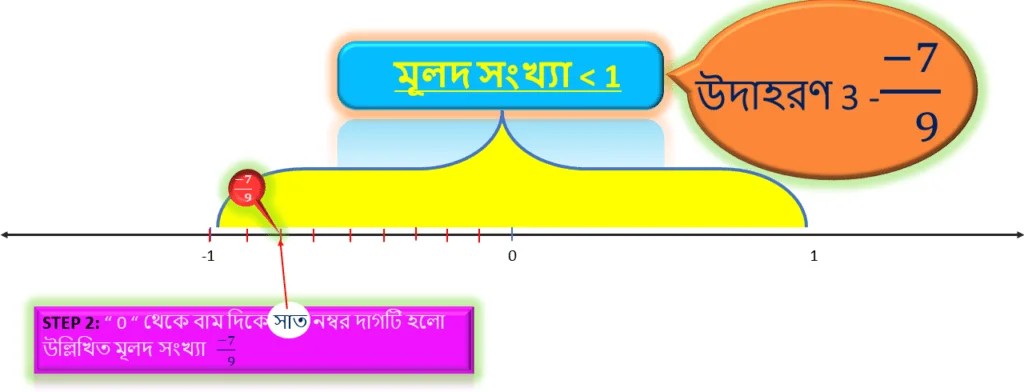
এরপর সংখ্যাটিতে দেখতে পাচ্ছি লব = 7 , অতএব এর আগে যে আমরা ” 0 ” থেকে ” -1 ” এর মধ্যের দূরত্বকে সমান ” 9 ” ভাগে ভাগ করেছি তার মধ্যে ” 0 ” থেকে বাম দিকে ছয় নাম্বার দাগ টি হবে উল্লিখিত মূলদ সংখ্যা -7/9 .
মূলদ সংখ্যার শ্রেণীবিভাগ
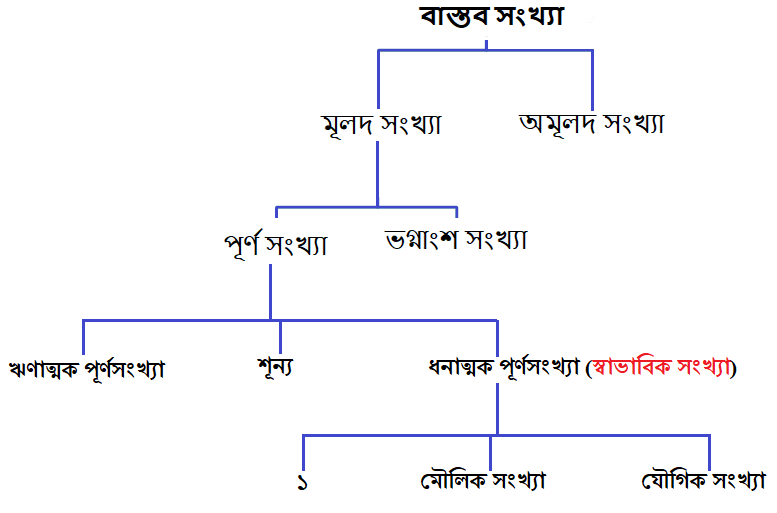
মূলদ সংখ্যা চেনার উপায়
- সকল পূর্ণ সংখ্যা-ই মূলদ সংখ্যা । যেমনঃ ২, ৪, ৫,৪৫,৭৬ ইত্যাদি মূলদ ।
- সকল ভগ্নাংশ আকারে লেখা যায় এমন সংখ্যা মূলদ সংখ্যা । ৫/৭, ৪ /৯ ইত্যাদি ।
- সসীম দশমিক ভগ্নাংশ সংখ্যা অর্থাৎ দশমিকের পরের অংক সংখ্যা যদি সসীম হয় তাহলে তা মূলদ সংখ্যা । যেমনঃ ৪.৫৬.৭.৪৮ ইত্যাদি ।
- প্রত্যেক পূর্ণসংখ্যা একটি মূলদ সংখ্যা। যেমন ৫ একটি মূলদ সংখ্যা, কারণ ৫ কে ভগ্নাংশ আকারে লেখা যাবে ৫/১, আমরা এটাও জানি সকল পূর্ণ সংখ্যার নিচে ১ থাকে।
- শূন্য, স্বাভাবিক সংখ্যা, প্রকৃত ও অপ্রকৃত ভগ্নাংশ সকলেই মূলদ সংখ্যা।
- যদি দশমিকের পরের ঘরগুলো সসীম হয় অর্থাৎগণনা করা যায়, তবে সংখ্যাটি হবে মূলদ সংখ্যা। যেমন:- ৩.৫৬ এবং ৫৬৯.৩৫ ইত্যাদি।
- সকল পৌণপৌনিক সংখ্যা মূলদ সংখ্যা।
- দশমিকের পরের ঘরগুলো যদি অভিন্ন আকারে অসীম হয় অর্থাৎ দশমিকের পরের সবগুলো সংখ্যা একই হলে তবে সংখ্যাটি মূলদ। যেমন:- ৫.৪৪৪…
- যে কোন পূর্ণবর্গ সংখ্যার বর্গমূল হলো মূলদ সংখ্যা। যেমন:- রুট ৩৬ এবং রুট ৪৯
- যেকোন পূর্নবর্গ সংখ্যা মূলদ সংখ্যা। যেমনঃ √৮১, √৩৬, √৬২৫ ইত্যাদি ।
- দশমিকের পরের অংক গুলো যদি অভিন্ন আকারে অসীম হয় বা আবৃত হয়, তাহলে তা মূলদ সংখ্যা । অর্থাৎ যে কোন আবৃত দশমিক ভগ্নাংশ ই মূলদ সংখ্যা।
মূলদ সংখ্যা বের করার নিয়ম
- মূলদ সংখ্যা বের করার জন্য, আমাদের কে মূলদ সংখ্যার বৈশিষ্টগুলো মিলিয়ে দেখতে হবে। মূলদ সংখ্যা বাছাই করার জন্য সংখ্যা ওপর নিম্নোক্ত উপায়গুলো প্রয়োগ করতে হবে।
- প্রত্যেক পূর্ণ সংখ্যা ই মূলদ সংখ্যা – তাই দেখতে হবে সংখ্যাটি পূর্ণ সংখ্যা কিনা পূর্ণ সংখ্যা হলে মূলদ সংখ্যা হিসাবে গন্য করতে হবে।
- তারপর দেখতে হবে কোন সংখ্যার দশমিক পরের অংকগুলো সসীম হলে তা মূলদ সংখ্যা হবে।
- দশমিকের পরের অংক গুলো যদি আবৃত হয় তাহলে সেটিও মূলদ সংখ্যা ।
- সবশেষে , যদি কোন পূর্নবর্গ সংখ্যার বর্গমূল থাকে তা মূলদ সংখ্যা হিসাবে গণ্য হবে।
০ কি মূলদ সংখ্যা
হ্যাঁ, 0 একটি মূলদ সংখ্যা কারণ এটিকে 0/1, 0/-2 ইত্যাদি পূর্ণসংখ্যার ভগ্নাংশ হিসাবে লেখা যেতে পারে। কারনঃ আমরা জানি , মূলদ সংখ্যাকে ভগ্নাংশ আকারে লেখা যায়। এখানে শূন্য (০) কে ভগ্নাংশ আকারে এভাবে লেখা যায় –
০/৫, ০/৪৫ ইত্যাদি । যেহেতু শূন্য (০) কে ভগ্নাংশ আকারে বা p/q আকারে লেখা যায়। p এবং q উভয়ই পূর্ন সংখ্যা আবার q এব মান শূন্য নয়।
সুতরাং শূন্য (০) একটি মূলদ সংখ্যা ।
আরো পড়তে: মৌলিক সংখ্যা কাকে বলে, গুণিতক কাকে বলে, গুণনীয়ক কাকে বলে
সমতুল্য মূলদ সংখ্যা কাকে বলে
সমতুল্য মূলদ সংখ্যার একটি সেট মানে মূলদ সংখ্যা যা ঠিক একই মান ধারণ করে।
একটি মূলদ সংখ্যাকে p/q আকারে প্রদত্ত শর্তে বর্ণনা করা যেতে পারে যে q শূন্যের সমান নয়। মূলদ সংখ্যার প্রদত্ত সেটটিকে একই বলা হয় যদি তাদের একই রূপগুলি একে অপরের সাথে মিলে যায়। সমতুল্য মূলদ সংখ্যার একটি সেট মানে মূলদ সংখ্যা যা ঠিক একই মান ধারণ করে, তবে বিভিন্ন আকারে উপস্থাপন বা চিত্রিত করা যেতে পারে। উদাহরণস্বরূপ, 24/30 এবং 4/5 সমতুল্য মূলদ সংখ্যা হিসাবে বিবেচিত হয়, কারণ পূর্ববর্তীটিকে পরবর্তীতে সরলীকরণ করা যেতে পারে।
মূলদ সংখ্যা ও অমূলদ সংখ্যা কাকে বলে
মূলদ সংখ্যা এর ইংরেজি হচ্ছে (Ratio) Nal Number । এখন দেখুন আমি Ratio শব্দটাকে আলাদা করে বলেছি ;
বোঝার সুবিধার জন্য ইংরেজিতে ratio মানে অনুপাত ; যেটা খাঁটি বাংলায় ভগ্নাংশ বলা যায়। কাজেই র্যাশনাল নাম্বার বা মূলদ সংখ্যা বলতে যে কোনো ভগ্নাংশ সংখা / ভগ্নাংশ আকারে প্রকাশ করা যায় এমন সংখ্যাকে বোঝায়। সুতরাং বুঝতেই পারছেন ৫/৬, ১/২ ইত্যাদি সব মূলদ সংখ্যা।
এখন আরেকটা বিষয় আপনাকে বলে রাখা ভালো যে পৌনঃপুনিক সংখ্যা নামে একরকমের সংখ্যা আছে যেটা দেখে আপনি দ্বিধায় পরতে পারেন যে এটা কিভাবে মূলদ সংখ্যা হয়। যে কোনো পৌনঃপুনিক সংখ্যাকে আপনি ভগ্নাংশের মাধ্যমে প্রকাশ করতে পারবেন।
যেমন আমি যদি বলি ০.৩৩৩৩৩৩৩৩৩৩৩৩৩….. এই সংখ্যাটা মূলদ কিনা… খেয়াল করুন এই সংখ্যাকে কিন্ত আমি ১/৩ এই আকারে প্রকাশ করতে পারি ; যেহেতু আগেই বলেছি যে যদি আপনি কোনো সংখ্যাকে ভগ্নাংশ আকারে প্রকাশ করতে পারেন তবেই সেটা মূলদ সংখ্যা।
মূলদ সংখ্যা কি
যে সকল সংখ্যাকে দুটি পূর্ণ সংখ্যার অনুপাতরূপে বা a/b আকারে প্রকাশ করা যায়, তাদেরকে মূলদ সংখ্যা (Rational number) বলে।
অর্থাৎ যে সকল সংখ্যাকে সাধারণ ভগ্নাংশ আকারে প্রকাশ করা যায়, তাকে মূলদ সংখ্যা বলে। একে Q দ্বারা প্রকাশ করা হয়।
অমূলদ সংখ্যা কি, অমূলদ সংখ্যা কাকে বলে
যে সকল সংখ্যাকে দুটি পূর্ণ সংখ্যার অনুপাতরূপে বা a/b আকারে প্রকাশ করা যায় না, তাদেরকে অমূলদ সংখ্যা (Irrational number) বলে।
অর্থাৎ যে সকল ভগ্নাংশ পূর্ণবর্গ নয়, তাই অমূলদ সংখ্যা। অসীম বা অনাবৃত্ত দশমিক সংখ্যাকে অমূলদ সংখ্যা বলে। একে Q’ দ্বারা প্রকাশ করা হয়। যেমন : √2, 3√11, √5, √7
অমূলদ সংখ্যা চেনার উপায়
- পূর্ণবর্গ নয় এমন যে কোন স্বাভাবিক সংখ্যার বর্গমূল অমূলদ সংখ্যা। রুট ৩, রুট ৫, রুট ৭ ইত্যাদি অমূলদ সংখ্যার উদাহরণ।
- দশমিকের পরের ঘরগুলো যদি ভিন্ন ভিন্ন আকারে অসীম হয় তবে সংখ্যাটি অমূলদ। যেমন:- ৭.৫৬৮৯…
মূলদ সংখ্যা ও অমূলদ সংখ্যার পার্থক্য
| মূলদ সংখ্যা | অমূলদ সংখ্যা |
|---|---|
| যে সকল ভগ্নাংশ পূর্ণবর্গ, তাই মূলদ সংখ্যা। | যে সকল ভগ্নাংশ পূর্ণবর্গ নয়, তাই অমূলদ সংখ্যা। |
| মূলদ সংখ্যাকে a/b আকারে প্রকাশ করা যায়। | অমূলদ সংখ্যাকে a/b আকারে প্রকাশ করা যায় না। |
| মূলদ সংখ্যায় দশমিকের পরের সংখ্যাগুলো সমীম হয় যেমন- ৪.৭৫, ৭.৮৬৯। | অমূলদ সংখ্যায় দশমিক চিহ্নের পরে অঙ্কগুলো পৌনঃপূণিক না হয়ে অসীম পর্যন্ত চলতে থাকে। যেমন : 3.125403128। |
| মূলদ সংখ্যার উদাহরণ √4, √9. √16, 3√8, 3√27। | অমূলদ সংখ্যার উদাহরণ √2, √3, √5, √11 |
| a/b পরস্পর সহমৌলিক হবে না, অর্থাৎ a/b এর গ.সা.গু. হবে কেবলমাত্র 1। | এদের ক্ষেত্রে দশমিকের পরের পুরো অংশটা অপরিমাপ যোগ্য । |
| প্রত্যেক সসীম সংখ্যাই মূলদ। | প্রত্যেক অসীম কিন্তু পৌনঃপুনিক নয়, এমন দশমিক সংখ্যা অমূলদ। |
FAQ | মূলদ সংখ্যা
Q1. মূলদ সংখ্যা কি
Ans – যে সংখ্যাকে দুটি পূর্ণ সংখ্যার অনুপাত হিসেবে প্রকাশ করা যায় তাকে মূলদ সংখ্যা বলে অর্থাৎ যে সংখ্যাকে ভগ্নাংশ আকারে প্রকাশ করা যায় তাকে মূলদ সংখ্যা বলে। যেমন:- ৫, ২/৩ ইত্যাদি।
Q2. 5 কি মূলদ সংখ্যা
Ans – আমরা জানি, 4 < 5 < 9,
∴ √4 < √5 < √9
বা, 2 < √5 < 3
প্রমাণঃ 2^(2 )=4, 〖(√5)〗^2=5, 3^2 =9
সুতারাং √5 এর মান 2 অপেক্ষা বড় এবং 3 অপেক্ষা ছোট।
অতএব, √5 পূর্ণ সংখ্যা নয়।
Q3. মূলদ সংখ্যা ইংরেজি
Ans – মূলদ সংখ্যা(Rational Number) হচ্ছে সেই সকল বাস্তব সংখ্যা যাদের ভগ্নাংশ আকারে প্রকাশ করা যায়।
Q4. 3 ও 4 এর মধ্যে দুটি মূলদ সংখ্যা লেখ
Ans – যেকোনো দুটি পৃথক সংখ্যার মধ্যেই অসীম সংখ্যক মূলদ সংখ্যা আছে।
এক্ষেত্রে (3/4).(3/4n)+(3/4)(1–1/3n), n=1,2,3,… আকারের সংখ্যাগুলিকে দিয়ে এদের মধ্যেকার মূলদ সংখ্যার সেটের একটা অসীম সাবসেট দেখালাম।
আপনি কি চাকরি খুজঁছেন, নিয়মিত সরকারি ও বেসরকারি চাকরির সংবাদ পেতে ক্লিক করুন। বিভিন্ন সরকারি ও বেসরকারি ক্ষেত্রে মানব সম্পদ উন্নয়ন সংক্রান্ত প্রতিবেদন পাড়ার জন্য, ক্লিক করুন। হিন্দিতে শিক্ষামূলক ব্লগ পড়তে, এখানে ক্লিক করুন। এছাড়াও, স্বাস্থ, টেকনোলজি, বিসনেস নিউস, অর্থনীতি ও আরো অন্যান্য খবর জানার জন্য, ক্লিক করুন। 



