কোণ কাকে বলে

কোন কাকে বলে, কোণ কাকে বলে কত প্রকার

দুইটি রেখাংশ পরস্পর প্রান্তবিন্দুতে মিলিত হয়ে যে জ্যামিতিক আকার ধারণ করে তাকে কোণ বলে। তাহলে সহজ করে বললে, দুইটি সরলরেখা পরস্পর মিলিত হলে কোণের উৎপন্ন হয়। এরূপ দুইটি সরলরেখা পরস্পর ছেদ করলে ছেদ বিন্দুতে চারটি কোণের উৎপন্ন হয়।

দুইটি রশ্মির প্রান্তবিন্দু পরস্পর মিলিত হলে মিলিত বিন্দুতে কোণ উৎপন্ন হয়। অন্যভাবে বললে, দুইটি রশ্মির প্রান্তবিন্দু পরস্পর মিলিত হয়ে যে আকৃতি ধারণ করে তাকে কোণ বলে।

আবার, দুইটি রেখাংশ পরস্পর প্রান্তবিন্দুতে মিলিত হয়ে যে জ্যামিতিক আকার ধারণ করে তাকে কোণ বলে। তাহলে সহজ করে বললে, দুইটি সরলরেখা পরস্পর মিলিত হলে কোণ উৎপন্ন হয়। এরূপ দুইটি সরলরেখা পরস্পর ছেদ করলে ছেদ বিন্দুতে চারটি কোণ উৎপন্ন হয়।

কোণের বৈশিষ্ট্য

• একটি কোণহতে ২ টি রশ্মির প্রয়োজন হয়।
• একটিকোণে একটি মাত্র শীর্ষ বিন্দু থাকে।
• একটি কোণের পরিমাণ ৩৬০º এর চেয়ে কখনোয় বড় হওয়া সম্ভব নয়।
• সাধারণ একটি কোণের দুটি বাহুতে একটি করে তীর বা অসীম চিহ্ন থাকে।
• একটি কোণের বাহু দুটি কে যত বড় বা ছোট করা হোক না কেন, কোণের পরিমাপের কোনো পরিবর্তন হয় না, অর্থাৎ কোণের পরিমাণ একই থাকে।
• কোনের পরিমাপের পরিবর্তন করতে হলে এর বাহু দুটি’র মধ্যকার দূরত্ব কম বা বেশি করতে হয়।
• তিনটি রেখা বা রশ্মি দ্বারা সর্বচ্চো ২ টিকোণ আকা সম্ভব।
• একটি কোণের শীর্ষ বিন্দু দিয়ে অন্য কোনো সরলরেখা চলে গেলে দুটি কোণের সৃষ্টি হয়।
• দুইটি সরলরেখা একে অপরকে ছেদ করে শুধুমাত্র চারটি কোণউৎপন্ন করতে পারে।
• একটি বিন্দুতে যেকোণ উৎপন্ন হয় তার পরিমাণ ৩৬০º বা দুই সরলকোণ বা চার সমকোণ।
• একটি বিন্দুতে যতোকোণ উৎপন্ন করা হোক না কেনো, কোণগুলোর সমষ্টি সবসময় ৩৬০º হবে।
• ত্রিভুজের তিন কোণের সমষ্টি বা যোগফল সবসময় ১৮০º হয়।
• চতুর্ভুজের কোণগুলোর যোগফল সবসময় ৩৬০º হয়।
• বর্গ ও আয়তের একটি বাহু অপর বাহুর সাথে সমকোণে মিলিত হয়।
• বর্গ ও রম্বসের কর্ণ গুলো পরস্পর সমকোণে একে অপরকে ছেদ করে।
• বৃত্তে অন্তর্লিখিত চতুর্ভুজের বিপরীত কোণগুলোর যোগফল ১৮০º হয়।

কোণের প্রকার

কোণের নির্দিষ্ট প্রকারভেদ করা একটু কঠিন। তবে আকার-আকৃতি, গঠন ও পরিমাপের ভিত্তিতে কোণের একটি তালিকা নিচে দেওয়া হলো

1. শুণ্যকোণ
2. সূক্ষ্মকোণ
3. সমকোণ
4. স্থূলকোণ
5. সরলকোণ
6. প্রবৃদ্ধকোণ
7. পূর্ণকোণ
8. তির্যককোণ
9. বিপ্রতীপকোণ
10. সন্নিহিতকোণ
11. পূরককোণ
12. সম্পূরককোণ
13. পরিপূরককোণ
14. অনুরূপকোণ
15. একান্তরকোণ
16. ধারাবাহিক অন্তঃস্থ কোণ

সূক্ষ্মকোণ

এক সমকোণ বা ৯০° অপেক্ষা ছোট কোণকে সূক্ষ্মকোণ বলে।

এক সমকোণ বা ৯০° অপেক্ষা ছোট কোণকে সূক্ষ্মকোণ বলে।

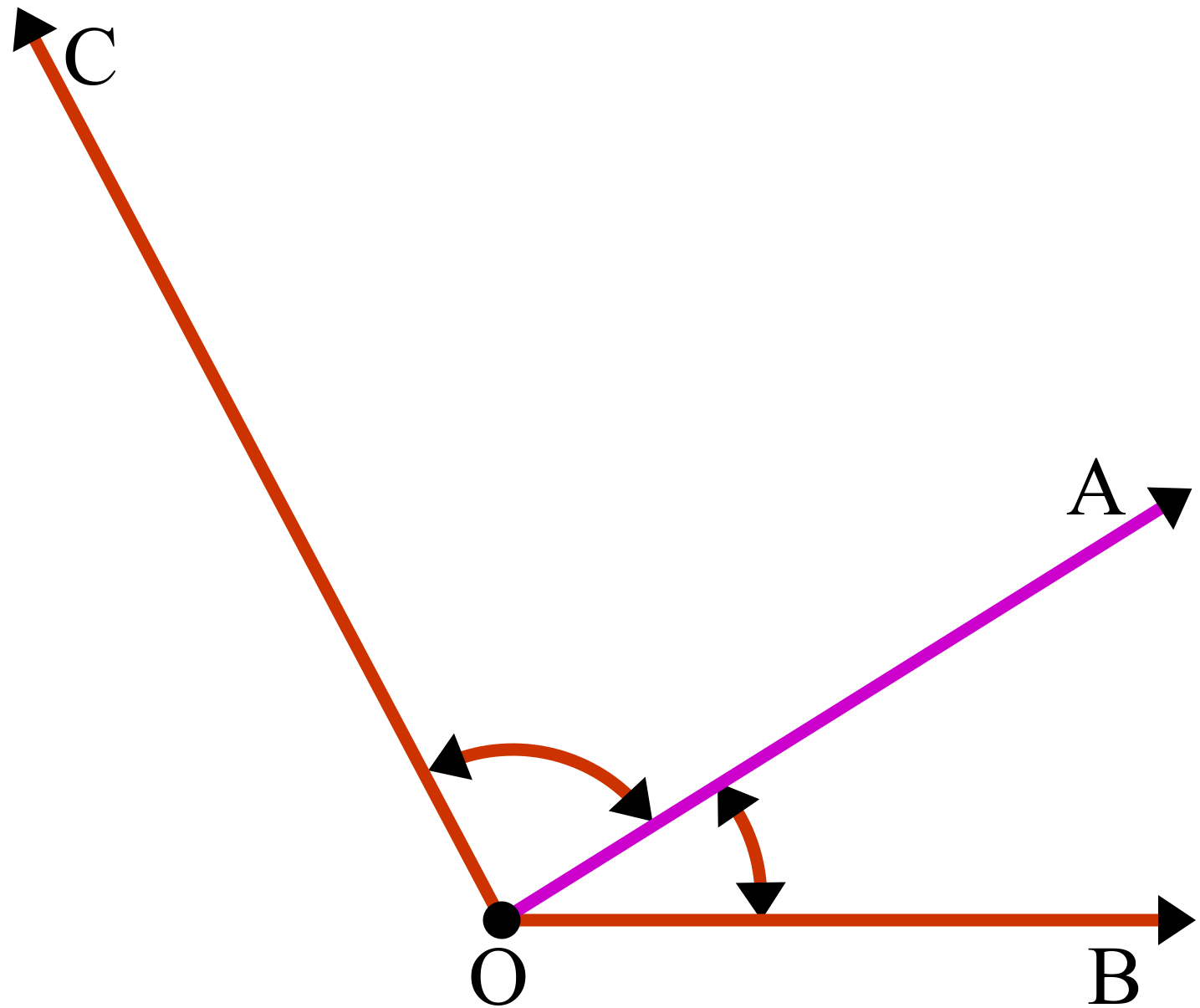
চিত্রে, OB রশ্মির সাথে ∠AOB এবং ∠COB দুইটি কোণ উৎপন্ন হয়েছে। এখানে CO⊥OB, অর্থাৎ ∠COB=৯০° এবং ∠AOB < ∠COB. সুতরাং, ∠AOB একটি সূক্ষ্মকোণ।

শুণ্যকোণ

যে কোণের পরিমাপ 0° তাকে শুণ্য কোণ বলে। এক্ষেত্রে, আসলে কোনো কোণ উৎপন্ন হয়নি।

দুইটি কোণের যোগফল ৩৬০° বা চার সমকোণ হলে কোণদুইটিকে পরস্পর পরিপূরককোণ বলে।

যে কোণের পরিমাপ 0° তাকে শুণ্য কোণ বলে। এক্ষেত্রে, আসলে কোনো কোণ উৎপন্ন হয়নি।

চিত্রে, OB রশ্মি প্রান্তবিন্দু O কে স্থির রেখে ঘড়ির কাটার বিপরীত দিকে ঘুড়ে OB অবস্থানে ∠BOB=0° কোণ উৎপন্ন করেছে। এখানে OB রশ্মি আদি অবস্থান থেকে কোনো দিকে না ঘুড়ে আদি অবস্থান OB -তেই আছে। ফলে কোনো কোণ উৎপন্ন হয়নি বা উৎপন্ন কোণের পরিমাপ 0°। অন্যভাবে বললে, OB রশ্মি প্রান্তবিন্দু O কে স্থির রেখে ঘড়ির কাটার বিপরীত দিকে ঘুড়ে OA অবস্থানে ∠AOB=0° কোণ উৎপন্ন করেছে। এখানে OA ও OB একই সরলরেখা বরাবর অবস্থান করছে। তাই উৎপন্ন কোণের পরিমান 0°।

অনুরূপকোণ, অনুরূপ কোণ কাকে বলে

দুইটি সমান্তরাল সরলরেখাকে অপর একটি ছেদক রেখা ছেদ করলে যে চার জোড়াকোণ উৎপন্ন হয়, তাদের মধ্যে ভিন্ন শীর্ষবিন্দু বিশিষ্ট যেসব কোণ জোড়া ছেদকের একই পাশে অবস্থান করে এবং কোণ দুইটির একটি অন্তঃস্থকোণ এবং অপরটি বহিঃস্থকোণ হয়, সেই কোণ জোড়াকে পরস্পর অনুরূপকোণ বলে।

দুইটি সমান্তরাল সরলরেখাকে অপর একটি ছেদক রেখা ছেদ করলে যে চার জোড়া কোণ উৎপন্ন হয়, তাদের মধ্যে ভিন্ন শীর্ষবিন্দু বিশিষ্ট যেসব কোণ জোড়া ছেদকের একই পাশে অবস্থান করে এবং কোণ দুইটির একটি অন্তঃস্থ কোণ এবং অপরটি বহিঃস্থ কোণ হয়, সেই কোণ জোড়াকে পরস্পর অনুরূপ কোণ বলে। অনুরূপ কোণকে আরেকভাবে সংজ্ঞায়িত করা যায় – তা হলোঃ

দুইটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে যে চার জোড়া বা আটটি কোণ উৎপন্ন হয়, তাদের মধ্যে প্রত্যেক জোড়ার অন্তর্গত কোণ দুইটিকে পরস্পর অনুরূপ কোণ বলা হয় যদি ও কেবল যদি তারা নিচের শর্তগুলো পূরণ করেঃ

• কোণ দুইটির শীর্ষবিন্দু ভিন্ন হয়।
• কোণ দুইটির উভয়েই ছেদকের একই পাশে অবস্থান করে।
• কোণ দুইটির একটি অন্তঃস্থ কোণ এবং অপরটি বহিঃস্থ কোণ হয়।

এরূপ চার জোড়া কোণ পাওয়া যায়।

একান্তরকোণ, একান্তর কোণ কাকে বলে

দুইটি সমান্তরাল সরলরেখাকে অপর একটি ছেদক রেখা ছেদ করলে যে চার জোড়াকোণ উৎপন্ন হয়, তাদের মধ্যে ভিন্ন শীর্ষবিন্দু বিশিষ্ট যেসবকোণ জোড়া ছেদকের বিপরীত পাশে অবস্থান করে এবং কোণ দুইটির উভয়েই অন্তঃস্থকোণ অথবা উভয়েই বহিঃস্থকোণ হয়, সেই কোণ জোড়াকে পরস্পর একান্তরকোণ বলে।

দুইটি সমান্তরাল সরলরেখাকে অপর একটি ছেদক রেখা ছেদ করলে যে চার জোড়া কোণ উৎপন্ন হয়, তাদের মধ্যে ভিন্ন শীর্ষবিন্দু বিশিষ্ট যেসব কোণ জোড়া ছেদকের বিপরীত পাশে অবস্থান করে এবং কোণ দুইটির উভয়েই অন্তঃস্থ কোণ অথবা উভয়েই বহিঃস্থ কোণ হয়, সেই কোণ জোড়াকে পরস্পর একান্তর কোণ বলে। একান্তর কোণকে অন্যভাবে সংজ্ঞায়িত করলে দাঁড়ায়ঃ

দুইটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে যে চার জোড়া বা আটটি কোণ উৎপন্ন হয়, তাদের মধ্যে প্রত্যেক জোড়ার অন্তর্গত কোণ দুইটিকে পরস্পর একান্তর কোণ বলা হয় যদি ও কেবল যদি তারা নিচের শর্তগুলো পূরণ করেঃ

• কোণ দুইটির শীর্ষবিন্দু ভিন্ন হয়।
• কোণ দুইটি ছেদকের বিপরীত পাশে অবস্থান করে।
• কোণ দুইটির উভয়েই অন্তঃস্থ কোণ অথবা উভয়েই বহিঃস্থ কোণ হয়।

এরূপ চার জোড়া কোণ পাওয়া যায়।

ধারাবাহিক অন্তঃস্থ কোণ

দুইটি সমান্তরাল সরলরেখাকে অপর একটি ছেদক রেখা ছেদ করলে যে চার জোড়াকোণ উৎপন্ন হয়, তাদের মধ্যে ভিন্ন শীর্ষবিন্দু বিশিষ্ট যে দুই জোড়া কোণ ছেদকের একই পাশে অবস্থান করে এবং কোণ দুইটির উভয়েই অন্তঃস্থকোণ হয়, সেই কোণ জোড়াকে পরস্পর ধারাবাহিক অন্তঃস্থকোণ বলে।

দুইটি সমান্তরাল সরলরেখাকে অপর একটি ছেদক রেখা ছেদ করলে যে চার জোড়া কোণ উৎপন্ন হয়, তাদের মধ্যে ভিন্ন শীর্ষবিন্দু বিশিষ্ট যে দুই জোড়া কোণ ছেদকের একই পাশে অবস্থান করে এবং কোণ দুইটির উভয়েই অন্তঃস্থ কোণ হয়, সেই কোণ জোড়াকে পরস্পর ধারাবাহিক অন্তঃস্থ কোণ বলে। ধারাবাহিক অন্তঃস্থ কোণকে অন্যভাবে সংজ্ঞায়িত করলে দাঁড়ায়ঃ

দুইটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা ছেদ করলে যে চার জোড়া বা আটটি কোণ উৎপন্ন হয়, তাদের মধ্যে যে দুই জোড়ার প্রত্যেক জোড়ার অন্তর্গত কোণ দুইটিকে পরস্পর ধারাবাহিক অন্তঃস্থ কোণ বলা হয় যদি ও কেবল যদি তারা নিচের শর্তগুলো পূরণ করেঃ

• কোণ দুইটির শীর্ষবিন্দু ভিন্ন হয়।
• কোণ দুইটি ছেদকের একই পাশে অবস্থান করে।
• কোণ দুইটির উভয়েই অন্তঃস্থ কোণ হয়।

এরূপ দুই জোড়া কোণ পাওয়া যায়।

সমকোণ, সমকোণ কাকে বলে

যে কোণের পরিমাপ ৯০° তাকে সমকোণ বলে।

যে কোণের পরিমাপ ৯০° তাকে সমকোণ বলে।

চিত্রে, OX রশ্মি আদি অবস্থান থেকে O বিন্দুতে ঘড়ির কাঁটার ঘূর্ণয়নের বিপরীত দিকে ঘুড়ে আবার OY অবস্থানে ∠XOY উৎপন্ন করেছে। এখানে ∠XOY= ৯০°।

সুতরাং, এটি একটি সমকোণ।

স্থূলকোণ

৯০° অপেক্ষা বড় এবং ১৮০° অপেক্ষা ছোট কোণকে স্থূলকোণ বলে। অন্যভাবে বলা যায়, সমকোণ অপেক্ষা বড় এবং সরলকোণ অপেক্ষা ছোট কোণকে স্থূলকোণ বলে।

৯০° অপেক্ষা বড় এবং ১৮০° অপেক্ষা ছোট কোণকে স্থূলকোণ বলে। অন্যভাবে বলা যায়, সমকোণ অপেক্ষা বড় এবং সরলকোণ অপেক্ষা ছোট কোণকে স্থূলকোণ বলে।

চিত্রে, AB রশ্মির O বিন্দুতে ∠BOC, ∠BOD এবং ∠AOB তিনটি কোণ উৎপন্ন হয়েছে। এখানে CO⊥AB, অর্থাৎ ∠BOC=৯০°. আবার, ∠AOB একটি সরলকোণ অর্থাৎ, ∠AOB=১৮০°. তাহলে, ∠BOC < ∠BOD < ∠AOB.

অর্থাৎ, ৯০°< ∠BOD < ১৮০°।

সুতরাং, ∠BOD একটি স্থূলকোণ।

সরলকোণ, সরল কোণ কাকে বলে

যে কোণের পরিমাপ ১৮০° তাকে সরলকোণ বলে।

যে কোণের পরিমাপ ১৮০° তাকে সরলকোণ বলে।

চিত্রে, AB একটি সরলরেখা এবং O, AB এর উপর একটি বিন্দু। O বিন্দুতে OC⊥AB. ফলে ∠AOC=∠BOC=90°. O বিন্দুতে আরেকটি ∠AOB উৎপন্ন হয়েছে। তাহলে,

∠AOB = ∠AOC + ∠BOC

বা, ∠AOB = ৯০° + ৯০°

∴ ∠AOB = ১৮০°

সুতরাং, ∠AOB একটি সরলকোণ।

প্রবৃদ্ধ কোণ, প্রবৃদ্ধ কোণ কাকে বলে

১৮০° অপেক্ষা বড় এবং ৩৬০° অপেক্ষা ছোট কোণকে প্রবৃদ্ধকোণ বলে। অন্যভাবে বলা যায়, সরলকোণ অপেক্ষা বড় এবং পূর্ণকোণ বা ৩৬০° অপেক্ষা ছোট কোণকে প্রবৃদ্ধকোণ বলে।

১৮০° অপেক্ষা বড় এবং ৩৬০° অপেক্ষা ছোট কোণকে প্রবৃদ্ধ কোণ বলে। অন্যভাবে বলা যায়, সরলকোণ অপেক্ষা বড় এবং পূর্ণ কোণ বা ৩৬০° অপেক্ষা ছোট কোণকে প্রবৃদ্ধ কোণ বলে।

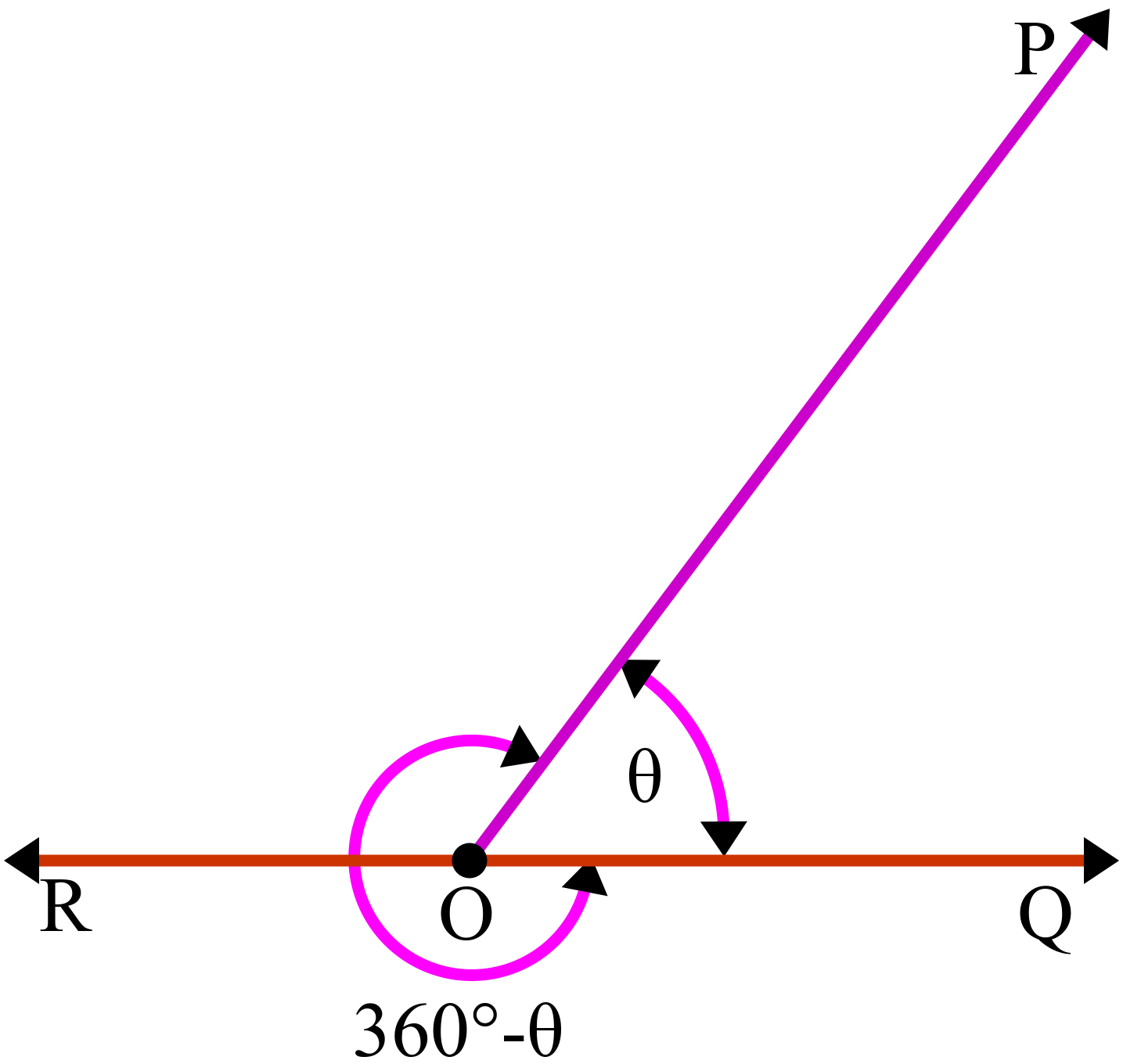
চিত্রে, OP রশ্মি আদি অবস্থান থেকে O বিন্দুতে ঘড়ির কাঁটার ঘূর্ণয়নের বিপরীত দিকে ঘুড়ে OQ অবস্থানে ∠POQ উৎপন্ন করেছে। আবার সরলকোণ ∠POR = ১৮০°। তাহলে, ∠POQ কোণটি ১৮০° অপেক্ষা বড় এবং ৩৬০° অপেক্ষা ছোট।

অর্থাৎ, ১৮০° < ∠POQ < ৩৬০°.

সুতরাং, ∠POQ একটি প্রবৃদ্ধ কোণ।

পূর্ণকোণ

যে কোণের পরিমাপ ৩৬০° তাকে পূর্ণকোণবলে। অন্যভাবে বলা যায়, একটি রশ্মি তার আদি অবস্থান থেকে ঘুরে আবার একই অবস্থান ফিরে আসলে যে কোণ উৎপন্ন হয় তাকে পূর্ণকোণ বলে। এ রকম একটি রশ্মি একবার ঘুরে আসলে রশ্মির প্রান্তবিন্দুতে উৎপন্ন কোণের পরিমাপ হয় ৩৬০°। তাই পূর্ণকোণের মান ৩৬০°।

যে কোণের পরিমাপ ৩৬০° তাকে পূর্ণকোণ বলে। অন্যভাবে বলা যায়, একটি রশ্মি তার আদি অবস্থান থেকে ঘুরে আবার একই অবস্থান ফিরে আসলে যে কোণ উৎপন্ন হয় তাকে পূর্ণকোণ বলে। এ রকম একটি রশ্মি একবার ঘুরে আসলে রশ্মির প্রান্তবিন্দুতে উৎপন্ন কোণের পরিমাপ হয় ৩৬০°। তাই পূর্ণকোণের মান ৩৬০°।

চিত্রে, OQ রশ্মি আদি অবস্থান থেকে O বিন্দুতে ঘড়ির কাঁটার ঘূর্ণয়নের বিপরীত দিকে ঘুড়ে আবার OQ অবস্থানে ফিরে আসলে উৎপন্ন কোণের পরিমান হয় θ = ৩৬০°।

অর্থাৎ, উৎপন্ন কোণের পরিমান θ হলে,

θ = ∠QOS + ∠SOP + ∠POT + ∠TOQ

বা, θ = ৯০° + ৯০° + ৯০° + ৯০°

∴ θ = ৩৬০°

সুতরাং, θ একটি পূর্ণকোণ।

তির্যককোণ

যে কোণের পরিমাপ ৯০° নয় বা ৯০° এর কোনো গুণিতক নয় তাকে তির্যককোণ বলে। অন্যভাবে বলা যায়, যে কোণের মান সমকোণের কোন গুণিতক নয় তাকে তির্যককোণ বলে। সেই হিসাবে, সব সূক্ষ্মকোণ এবং স্থূলকোণই এক একটি তির্যককোণ বলে পরিচিত।

যে কোণের পরিমাপ ৯০° নয় বা ৯০° এর কোনো গুণিতক নয় তাকে তির্যক কোণ বলে। অন্যভাবে বলা যায়, যে কোণের মান সমকোণের কোন গুণিতক নয় তাকে তির্যক কোণ বলে। সেই হিসাবে, সব সূক্ষ্মকোণ এবং স্থূলকোণ এক একটি তির্যক কোণ বলে পরিচিত।

চিত্রে, OB রশ্মির সাথে O বিন্দুতে ধনাত্মক দিকে অর্থাৎ, ঘড়ির কাঁটার ঘূর্ণয়নের বিপরীত ∠BOE একটি সূক্ষ্মকোণ, ∠BOF একটি স্থূলকোণ এবং ∠BOG ও ∠BOH আরও দুইটি প্রবৃদ্ধ কোণ উৎপন্ন করেছে। কোণগুলোর কোনটিই সমকোণ বা ৯০° নয় এবং কোনটিই সমকোণের গুণিতকও নয়। তাই এরা সবাই এক একটি তির্যক কোণ। আবার,

∠BOC = ৯০°,

∠BOA = ১৮০°

∴ ∠BOA = ২ × ৯০°,

∠BOD = ২৭০°

∴ ∠BOD = ৩ × ৯০°,

∠BOB = ৩৬০° [∵ একটি পরিপূর্ণ ঘূর্ণন = পূর্ণ কোণ]

∴ ∠BOB = ৪ × ৯০°

দেখা যাচ্ছে যে, ∠BOC, ∠BOA, ∠BOD এবং ∠BOB এরা সবাই সমকোণের এক একটি গুণিতক । সুতরাং, এদের কোনটিই তির্যক কোণ নয়। অতএব, সমকোণ, সরলকোণ এবং পূর্ণকোণ কেউই তির্যক কোণ নয়।

বিপ্রতীপকোণ, বিপ্রতীপ কোণ কাকে বলে

একটি কোণের বিপরীত রশ্মি দুইটি ঐ কোণের বিপরীতে যে কোণ উৎপন্ন করে তাকে পূর্বের কোণের বিপ্রতীপকোণ বলে। অন্যভাবে বলা যায়, দুইটি পরস্পরচ্ছেদী সরলরেখা কোনো একটি বিন্দুতে মিলিত হলে, মিলিত বিন্দুতে দুই জোড়া বিপরীতকোণ উৎপন্ন হয়, প্রতিজোড়া বিপরীত কোণের একটিকে অপরটির বিপ্রতীপকোণ বলে। বিপ্রতীপ কোণদ্বয় পরস্পর সমান হয়।

একটি কোণের বিপরীত রশ্মি দুইটি ঐ কোণের বিপরীতে যে কোণ উৎপন্ন করে তাকে পূর্বের কোণের বিপ্রতীপ কোণ বলে। অন্যভাবে বলা যায়, দুইটি পরস্পরচ্ছেদী সরলরেখা কোনো একটি বিন্দুতে মিলিত হলে, মিলিত বিন্দুতে দুই জোড়া বিপরীত কোণ উৎপন্ন হয়, প্রতিজোড়া বিপরীত কোণের একটিকে অপরটির বিপ্রতীপ কোণ বলে। বিপ্রতীপ কোণদ্বয় পরস্পর সমান হয়।

চিত্রে, AB ও CD সরলরেখা দুইটি পরস্পর O বিন্দুতে ছেদ করেছে। ফলে O বিন্দুতে ∠AOD, ∠AOC, ∠COB, এবং ∠BOD চারটি কোণ উৎপন্ন হয়েছে। আবার, ∠AOD কোণের বাহু দুইটির বিপরীত রশ্মি দ্বারা ∠COB উৎপন্ন হয়েছে। সুতরাং, ∠AOD এর বিপ্রতীপ ∠COB.

তদ্রূপ, ∠AOC কোণের বাহু দুইটির বিপরীত রশ্মি দ্বারা ∠BOD উৎপন্ন হয়েছে। সুতরাং, ∠AOC এর বিপ্রতীপ ∠BOD.

আবার, বিপ্রতীপ কোণগুলো পরস্পর সমান।

সুতরাং, ∠AOD = ∠COB এবং ∠AOC = ∠BOD.

সন্নিহিতকোণ, সন্নিহিত কোণ কাকে বলে

একই সমতলে অবস্থিত দুইটি কোণের শীর্ষবিন্দু ও একটি রশ্মি যদি সাধারণ হয় এবং কোণ দুইটি, সাধারণ রশ্মির বিপরীত দিকে অবস্থান করে, তবে কোণদুইটিকে পরস্পর সন্নিহিতকোণ বলে। যদি একই শীর্ষবিশিষ্ট দুইটি কোণের একটি সাধারণ বাহু থাকে এবং কোণ দুইটির কোনো অভ্যন্তরস্থ বিন্দু সাধারণ না হয়, তাহলে কোণ দুইটিকে পরস্পর সন্নিহিতকোণ বলে।

একই সমতলে অবস্থিত দুইটি কোণের শীর্ষবিন্দু ও একটি রশ্মি যদি সাধারণ হয় এবং কোণ দুইটি, সাধারণ রশ্মির বিপরীত দিকে অবস্থান করে, তবে কোণ দুইটিকে পরস্পর সন্নিহিত কোণ বলে। যদি একই শীর্ষবিশিষ্ট দুইটি কোণের একটি সাধারণ বাহু থাকে এবং কোণ দুইটির কোনো অভ্যন্তরস্থ বিন্দু সাধারণ না হয়, তাহলে কোণ দুইটিকে পরস্পর সন্নিহিত কোণ বলে।

চিত্রে, OA এবং OB রশ্মিদ্বয় O বিন্দুতে ∠AOB উৎপন্ন করেছে। আবার, OA এবং OC রশ্মিদ্বয় O বিন্দুতে ∠AOC উৎপন্ন করেছে। উভয় কোণের শীর্ষবিন্দু O সাধারণ এবং উভয় কোণের সাধারণ বাহু OA. আবার কোণ দুইটি, সাধারণ বাহু OA বিপরীত দিকে অবস্থিত। তাছাড়া কোণ দুইটির অভ্যন্তরস্থ কোনো বিন্দু সাধারণ নয়। অতএব, কোণ দুইটি পরস্পর সন্নিহিত কোণ।

সুতরাং, ∠AOB এবং ∠AOC কোণ দুইটি সন্নিহিত কোণ।

পূরককোণ, পূরক কোণ কাকে বলে

দুইটি কোণের যোগফল ৯০° বা এক সমকোণ হলে কোণ দুইটির একটিকে অপরটির পূরককোণ বলে। পরস্পর পূরককোণ দুইটি যদি সন্নিহিত কোণ হয়, তবে সন্নিহিতকোণ দুইটির সাধারণ বাহু ব্যতীত অপর বাহু দুইটি বাহু পরস্পর লম্ব হয়। ইউক্লিডিও জ্যামিতি অনুযায়ী, একটি সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের একটি অপরটির পূরককোণ।

দুইটি কোণের যোগফল ৯০° বা এক সমকোণ হলে কোণ দুইটির একটিকে অপরটির পূরক কোণ বলে। পরস্পর পূরক কোণ দুইটি যদি সন্নিহিত কোণ হয়, তবে সন্নিহিত কোণ দুইটির সাধারণ বাহু ব্যতীত অপর বাহু দুইটি বাহু পরস্পর লম্ব হয়। ইউক্লিডিও জ্যামিতি অনুযায়ী, একটি সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের একটি অপরটির পূরক কোণ। কারণ মনেকরি, সমকোণী ত্রিভুজ ABC -এ ∠B = ৯০°। আবার ত্রিভুজের তিনকোণের সমষ্টি ১৮০°.

∴ ∠A + ∠B + ∠C = ১৮০°

বা, ∠A + ৯০° + ∠C = ১৮০°

বা, ∠A + ∠C = ১৮০° – ৯০°

∴ ∠A + ∠C = ৯০°

অতএব, ∠A এবং ∠C পরস্পর পূরক কোণ।

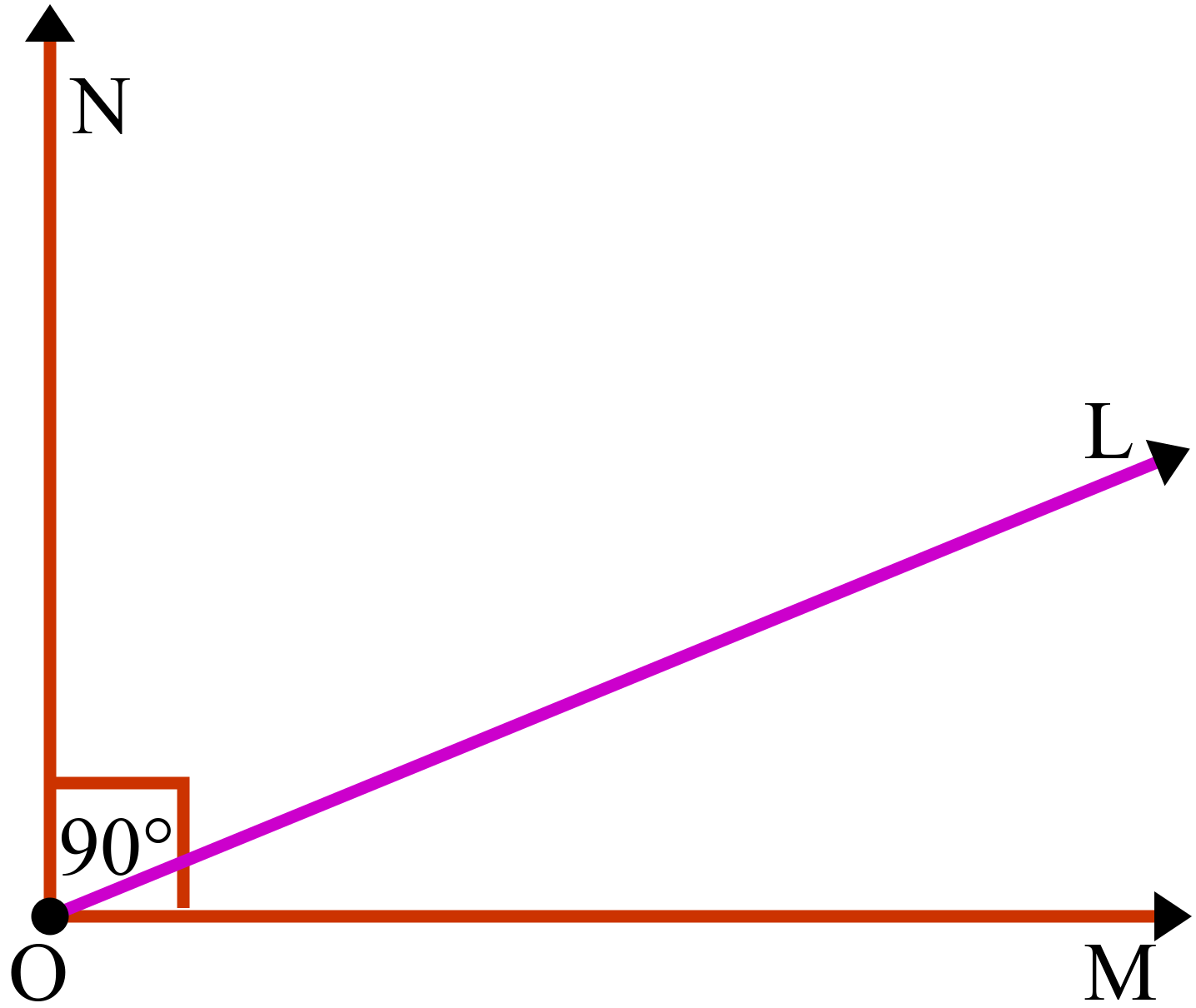
চিত্রে, OM রশ্মির O বিন্দুতে ∠MOL এবং ∠LON দুইটি কোণ উৎপন্ন হয়েছে। এখন, ∠MOL + ∠LON = এক সমকোণ বা ৯০°।

সম্পূরককোণ, সম্পূরক কোণ কাকে বলে

দুইটি কোণের যোগফল ১৮০° বা দুই সমকোণ হলে কোণ দুইটির একটিকে অপরটির সম্পূরককোণ বলে।

দুইটি কোণের যোগফল ১৮০° বা দুই সমকোণ হলে কোণ দুইটির একটিকে অপরটির সম্পূরক কোণ বলে। অতএব পরস্পর সম্পূরক কোণ দুইটির সমষ্টি একটি সরলকোণ তৈরি করে। পরস্পর সম্পূরক কোণ দুইটি যদি সন্নিহিত কোণ হয়, তবে সন্নিহিত কোণ দুইটির সাধারণ বাহু ব্যতীত অপর বাহু দুইটি একই সরলরেখায় অবস্থিত হয়। এই ক্ষেত্রে, কোণ দুইটি রৈখিক যুগল কোণ বলেও পরিচিত। সম্পূরক কোণ দুইটি একই রেখায় হতে হবে – এমন কোনো শর্ত নেই। সম্পূরক কোণ দুইটি আলাদা দুই জায়গাতেও থাকতে পারে। যেমন – সামান্তরিকের সন্নিহিত কোণ দুইটি পরস্পর সম্পূরক। আরও একটু সুস্পষ্ট করে বললে, ABCD একটি সামান্তরিক হলে, এর যেকোনো বাহু সংলগ্ন কোণ দুইটির যোগফল ১৮০°. আবার বৃত্তে অন্তর্লিখিত চতুর্ভুজের যে কোনো দুইটি বিপরীত কোণ পরস্পর সম্পূরক। অর্থাৎ, বৃত্তে অন্তর্লিখিত চতুর্ভুজের যে কোনো দুইটি বিপরীত কোণের সমষ্টি দুই সমকোণ বা ১৮০°।

চিত্রে, XY রেখার O বিন্দুতে ∠YOZ এবং ∠ZOX দুইটি কোণ উৎপন্ন হয়েছে। এখন, ∠YOZ + ∠ZOX = সরলকোণ বা ১৮০°।

সুতরাং, ∠YOZ এবং ∠ZOX কোণ দুইটি পরস্পর সম্পূরক।

তাছাড়া, কোণ দুইটি পরস্পর সন্নিহিত কোণ।

পরিপূরককোণ

দুইটি কোণের যোগফল ৩৬০° বা চার সমকোণ হলে কোণ দুইটিকে পরস্পর পরিপূরককোণ বলে।

দুইটি কোণের যোগফল ৩৬০° বা চার সমকোণ হলে কোণ দুইটিকে পরস্পর পরিপূরক কোণ বলে।

একান্তর কোণ কাকে বলে

দুটি সমান্তরাল রেখাকে অপর একটি রেখা তির্যকভাবে ছেদ করলে ছেদ রেখার বিপরীত পাশে সমান্তরাল রেখা যে কোণ উৎপন্ন করে তাকে, একান্তর কোণ বলে।

দু’টি সমান্তরাল রেখাকে অপর একটি রেখা তির্যকভাবে ছেদ করলে ছেদক রেখার বিপরীত পাশে সমান্তরাল রেখা যে কোণ উৎপন্ন করে তাকে একান্তর কোণ বলে। একান্তর কোণগুলো পরস্পর সমান হয়।

চিত্রে, MN এবং OP সরলরেখা দুইটিকে QR সরলরেখা যথাক্রমে S এবং T বিন্দুতে ছেদ করেছে। ফলে S এবং T বিন্দু হলো ছেদক রেখার সাথে দুইটি ছেদ বিন্দু। S বিন্দুতে দুইজোড়া এবং T বিন্দুতে আরও দুইজোড়া করে মোট চার জোড়া কোণ উৎপন্ন হয়েছে। QR সরলরেখাটি উভয় সরলরেখাকে ছেদ করেছে বলে QR সরলরেখাকে ছেদক রেখা বলা হয়।

∠NSR এবং ∠QTO কোণ দুইটি বিশ্লেষণ করলে দেখা যায় যে, উভয় কোণের শীর্ষবিন্দুই ভিন্ন এবং উভয় কোণই ছেদক রেখা PQ এর বিপরীত পাশে অবস্থিত। তাছাড়া, উভয় কোণই অন্তঃস্থ কোণ। তাই এই কোণ দুইটি পরস্পর একান্তর কোণ। তেমনিভাবে ∠MSR এবং ∠QTP কোণ জোড়াও পরস্পর একান্তর কোণ।

এখন, ∠NSR এবং ∠QTO পরস্পর একান্তর কোণ হওয়ার কারণে তারা পরস্পর সমান।

∴ ∠NSR = ∠QTO.

আবার, ∠MSR এবং ∠QTP পরস্পর একান্তর কোণ বলে কোণ দুইটি পরস্পর সমান।

∴ ∠MSR = ∠QTP.

উপরে উল্লেখিত একান্তর কোণের সংজ্ঞা সমান্তরাল সরলরেখা বিবেচনা করে দেওয়া হয়েছে। তবে সমান্তরাল সরলরেখা ছাড়াও একান্তর কোণকে সংজ্ঞায়িত করা যায় যা একান্তর কোণের সাধারণ সংজ্ঞা বলে অভিহিত। একান্তর কোণের সাধারণ সংজ্ঞা হলো নিম্নরূপঃ

একজোড়া সরলরেখাকে আরেকটি ছেদক সরলরেখা ছেদ করলে উভয় ছেদবিন্দুতে যে চার জোড়া কোণ উৎপন্ন হয়, তাদের মধ্যে ভিন্ন শীর্ষবিন্দু বিশিষ্ট যেসব জোড়া কোণ ছেদক রেখার বিপরীত পার্শ্বে বিরাজমান এবং কোণ দুইটির উভয়েই অন্তঃস্থ কোণ অথবা উভয়েই বহিঃস্থ কোণ হয়, সেসব কোণ জোড়ার একটিকে অপরটির পরস্পর একান্তর কোণ বলে।

কোণের নামকরণের নিয়ম

যে বিন্দুতে কোণ উৎপন্ন হয় সেই বিন্দুকে মাঝখানে লিখতে হয় । তার দুই পাশে ধারক বাহু দুটির অপর প্রান্তবিন্দু দুটি লিখতে হয় ।

কোণ পরিমাপের একক

এক সমকোণের ৭০ ভাগের এক ভাগকে বলে এক ডিগ্রি (1°) । আবার ডিগ্রিকে মিনিট,

সেকেন্ডে ভাগ করা হয় ।

যেমন— 1 সমকোণ = 90°

1 ডিগ্রি (1° ) = 60 মিনিট ( 60 )

1 মিনিট ( 1′ ) = 60 সেকেন্ড ( 60” )

রেডিয়ান বলতে বোঝায় কোনো বৃত্তের ব্যাসার্ধের সমান বৃত্তচাপ কেন্দ্রে যে কোণ উৎপন্ন করে, তার পরিমাণকে বলে এক রেডিয়ান বা 1 ।

রেডিয়ান ও ডিগ্রির মধ্যে সম্পর্ক

180° = n° ( পাই রেডিয়ান )

আরো অন্যান্য অতি জনপ্রিয় প্রশ্নোত্তর সম্পর্কে জানার জন্য এখানে ক্লিক করুন 

FAQ | কোণ কাকে বলে

আপনি কি চাকরি খুজঁছেন, নিয়মিত সরকারি ও বেসরকারি চাকরির সংবাদ পেতে ক্লিক করুন। বিভিন্ন সরকারি ও বেসরকারি ক্ষেত্রে মানব সম্পদ উন্নয়ন সংক্রান্ত প্রতিবেদন পাড়ার জন্য, ক্লিক করুন। হিন্দিতে শিক্ষামূলক ব্লগ পড়তে, এখানে ক্লিক করুন। এছাড়াও, স্বাস্থ, টেকনোলজি, বিসনেস নিউস, অর্থনীতি ও আরো অন্যান্য খবর জানার জন্য, ক্লিক করুন।