ত্রিভুজ কাকে বলে, সমকোণী ত্রিভুজ কাকে বলে, সমবাহু ত্রিভুজ কাকে বলে,সূক্ষ্মকোণী ত্রিভুজ কাকে বলে

ত্রিভুজ কাকে বলে, ত্রিভুজ কাকে বলে চিত্র সহ

ত্রিভুজ, শব্দটি একটি পুরানো ল্যাটিন শব্দ “ট্রায়াঙ্গুলাম” থেকে এসেছে যার অর্থ তিনকোনা। ত্রিভুজ হল মৌলিক আকার যা আমরা আমাদের দৈনন্দিন জীবনে দেখতে পাই।

পিজ্জার টুকরো, কাছাকাছি পাহাড়, আপনার বাড়ির ছাদ সবই ত্রিভুজ যদি আপনি তাদের 2-মাত্রিক ছবিগুলি দেখেন।

গণিতের জ্যামিতিতে, আমরা বিভিন্ন ধরনের আকৃতি দেখতে পাই – কিছু দ্বিমাত্রিক এবং কিছু ত্রিমাত্রিক। যে আকৃতি দুটি প্যারামিটারের সাহায্যে সংজ্ঞায়িত করা যায় তাকে দ্বিমাত্রিক আকৃতি বলা হয় এবং যেগুলিকে তিনটি প্যারামিটার দিয়ে সংজ্ঞায়িত করা যায় সেগুলিকে ত্রিমাত্রিক আকার বলা হয়।

দ্বি-মাত্রিক আকারের মধ্যে রয়েছে বর্গাকার, আয়তক্ষেত্র, ত্রিভুজ ইত্যাদি। একটি বহুভুজ হল এমন একটি দ্বি-মাত্রিক কাঠামো যার বাহু রয়েছে। একটি ত্রিভুজ তিনটি লাইন সেগমেন্টের যেকোন জোড়ার জন্য একটি নির্দিষ্ট কোণে স্থাপন করা তিনটি রেখার অংশ নিয়ে গঠিত।

একটি ত্রিভুজের তিনটি কোণ রয়েছে যার যোগফল ধ্রুবক যা 180°। একটি ত্রিভুজ △PQR হয়। △PQR-এর কোণের সমষ্টি হল 180°। তাই, ∠P + ∠Q + ∠R = 180°। আসুন এখন ত্রিভুজগুলির মূল বিষয়গুলি অধ্যয়ন করি।

ত্রিভুজ কাকে বলে

সমতলস্থ তিনটি বিন্দু যদি সমরেখ না হয় তবে তাদের দুইটি করে সংযোগ করে প্রান্ত রেখাংশ তিনটির সংযোগকে একটি ত্রিভুজ বলা হয়।

সমতলস্থ A. B. C বিন্দু তিনটি যদি সমরেখ না হয় A ও B, B ও C এবং C ও A, এর সংযোজক রেখাংশ তিনটি দ্বারা ABC ত্রিভুজ গঠিত হয় এবং ABC প্রতীক দ্বারা নির্দেশ করা হয়। A,B,C বিন্দু তিনটিকে ABC-এর শীর্ষবিন্দু এবং AB, BC, CA রেখাংশ তিনটিকে তার বাহু বলা হয়।

তিনটি রেখাংশ দ্বারা আবদ্ধ চিত্র একটি ত্রিভুজ। রেখাংশগুলোকে ত্রিভুজের বাহু বলে। যেকোনো দুইটি বস্তুর সাধারণ বিন্দুকে শীর্ষবিন্দু বলা হয়। ত্রিভুজের যেকোনো দুইটি বাহু শীর্ষবিন্দুতে কোণ উৎপন্ন করে। ত্রিভুজের তিনটি বাহু ও তিনটি কোণ রয়েছে।

ত্রিভুজের বাহু তিনটির দৈর্ঘ্যের সমষ্টিকে পরিসীমা বলে। অর্থাৎ AB, BC, CA বাহুর পরিমাপের সমষ্টি ত্রিভুজটির পরিসীমা ।

ত্রিভুজের বাহুগুলো দ্বারা সীমাবদ্ধক্ষেত্রকে ত্রিভুজক্ষেত্র বলে।

ত্রিভুজের যেকোনো শীর্ষবিন্দু হতে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত অঙ্কিত রেখাংশকে মধ্যমা বলে। প্রত্যেক ত্রিভুজের তিনটি মধ্যমা আছে।

আবার, যেকোনো শীর্ষবিন্দু হতে বিপরীত বাহু এর লম্ব দূরত্বই ত্রিভুজের উচ্চতা।

চিত্রে, ABC একটি ত্রিভুজ এবং A, B ও C ত্রিভুজটির তিনটি শীর্ষবিন্দু। AB, BC, CA ত্রিভুজের তিনটি বাহু এবং <BAC, <ABC, <BCA তিনটি কোণ।

সুতরাং, একটি ত্রিভুজ তিনটি শীর্ষবিন্দু, তিনটি বাহু ও তিনটি কোনের সমন্বয়ে গঠিত।

ত্রিভুজের বৈশিষ্ট্য

ত্রিভুজের কিছু বৈশিষ্ট্য নিম্নরূপ-

1. ত্রিভুজের তিনটি কোণের যোগ 180 ডিগ্রি হয়। এর কারণ হল একটি সম্পূর্ণ বৃত্তের কোণ যোগ 360 ডিগ্রি। ত্রিভুজ হল ঐ বৃত্তের অর্ধেক। সুতরাং ত্রিভুজের কোণ যোগ 180 ডিগ্রি।

2. ত্রিভুজের তিনটি বাহু থাকে যা তিনটি কোণের মধ্যে বিভক্ত হয়।

3. প্রতিটি ত্রিভুজের তিনটি কৌণিক বিন্দু থাকে, যেগুলো ত্রিভুজের তিনটি বাহুর সংগ্রহস্থল।

4. ত্রিভুজের যেকোন দুই বাহুর যোগ, তৃতীয় বাহু অপেক্ষা বৃহত্তর হয়।

5. ত্রিভুজের যেকোন দুই বাহুর বিয়োগ, তৃতীয় বাহু অপেক্ষা ছোট হয়।

6. সমবাহু ত্রিভুজে তিনটি বাহু এবং তিনটি কোণ পরস্পর সমান হয়।

7. সমকোণী ত্রিভুজে প্রতিটি কোণের পরিমাপ 60 ডিগ্রি হয়।

8. পরিকেন্দ্র হল ত্রিভুজের তিনটি বাহুর লম্বসমষ্টির মধ্যবিন্দু।

9. মধ্যমা হল শীর্ষবিন্দু হতে বিপরীত বাহুর মধ্যবিন্দুর দূরত্ব।

10. লম্ববিন্দু হল শীর্ষবিন্দু হতে বিপরীত বাহুর উপর অঙ্কিত লম্ব।

11. ত্রিভুজের কোন একটি বাহু অপর একটি বাহু অপেক্ষা বড় হলে, বড় বাহুর বিপরীত কোণটি ছোট বাহুর বিপরীত কোণ অপেক্ষা বড় হয়।

12. ত্রিভুজের দুইটি কোণ সমান হলে, সেই দুইটি কোণের বিপরীত দুইটি বাহুও সমান হয়।

13. ত্রিভুজের দুইটি বাহু সমান হলে, সেই দুইটি বাহুর বিপরীত দুইটি কোণও সমান হয়।

14. ত্রিভুজের ভিতরে অঙ্কিত তিনটি বৃত্তের কেন্দ্র এক সোজা রেখায় অবস্থিত থাকে।

15. ত্রিভুজের ভিতরে অঙ্কিত বৃত্তগুলোর ব্যাসাবলী পরস্পর সমান্তরাল হয়।

ত্রিভুজের ক্ষেত্রফলের সূত্র, ত্রিভুজের ক্ষেত্রফলের সূত্র কি

”কোন একটি সমকোণী ত্রিভুজের অতিভুজ এর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল। ঐ ত্রিভুজের অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্র দ্বয়ের ক্ষেত্রফলের সমষ্টির সমান।”

যেমন, (a2 + b2 = c2), যেখানে a এবং b হল পায়ের দৈর্ঘ্য এবং c হল অতিভূজের দৈর্ঘ্য।

• ত্রিভুজের ভূমি ও উচ্চতা দেওয়া থাকলে ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র, = (1/2)×ভূমি×উচ্চতা
• ত্রিভুজটি ৩ টি বাহুর দৈর্ঘ্য দেওয়া থাকলে ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র, = √(s(s-a)(s-b)(s-c)); এখানে s=(a+b+c)/2
• ত্রিভুজটি সমবাহু হলে ক্ষেত্রফল = (√3/4)a²
• ত্রিভুজটি সমদ্বিবাহু হলে ক্ষেত্রফল = (b²/4)√(4a²-b²)

ত্রিভুজের পরিসীমা নির্ণয়ের সূত্র

ত্রিভুজের পরিসীমা হলো ত্রিভুজের বাহুগুলোর সমষ্টি। মনেকরি, ABC একটি ত্রিভুজ যার বাহু তিনটির পরিমাপ a একক, b একক, c একক এবং পরিসীমা P একক। তাহলে ত্রিভুজের পরিসীমার সূত্র হবে,
P = (a + b + c) একক।

যে কোনো ত্রিভুজের পরিসীমা = তিনটি বাহুর দৈর্ঘ্যের যোগফল

একটি ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a একক, b একক, c একক এবং পরিসীমা P একক হলে,
P = (a + b + c) একক।

ত্রিভুজের ভূমি নির্ণয়ের সূত্র কি

সূত্রটি হলো,

কোন সমকোনী ত্রিভুজ এর অতিভুজের উপর অঙ্কিত বর্গক্ষেত্র অপর 2 বাহুর উপর অঙ্কিত বর্গক্ষেত্রের সমষ্টির সমান। অর্থাৎ : (অতিভূজ^2= লম্ব^2+ভূমি^2).

(ক্ষেত্রফল÷উচ্চতা)×২

ত্রিভুজ কত প্রকার, ত্রিভুজের প্রকারভেদ

বাহুভেদে ত্রিভূজ তিন প্রকার।

1. সমবাহু ত্রিভুজ,
2. সমদ্বিবাহু ত্রিভুজ ও
3. বিষমবাহু ত্রিভূজ ।

আবার, কোনভেদেও ত্রিভূজ তিন প্রকার।

1. সুক্ষ্মকোণী ত্রিভুজ,
2. স্থূলকোণী ত্রিভুজ ও
3. সমকোণী ত্রিভূজ।

বাহুভেদে ত্রিভূজ কয় প্রকার ও কি কি

বাহুভেদে ত্রিভূজ তিন প্রকার যা উপরে জানা গেছে, এবার এই তিন প্রকার ত্রিভূজ সম্পর্কে বিস্তারিত আলোচনা করা হলো

সমবাহু ত্রিভুজ কাকে বলে

যে ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যই সমান, তাকে সমবাহু ত্রিভুজ বলে।

উলেখ্য সমবাহু ত্রিভুজের তিনটি কোণের পরিমাণও সমান।

চিত্রে, ABC ত্রিভুজটি একটি সমবাহু ত্রিভুজ, যার AB বাহু = BC বাহু = CA বাহু সমান।

সমবাহু ত্রিভুজের বৈশিষ্ট্য

১. সমবাহু ত্রিভুজের তিনটি বাহু পরস্পর সমান দৈর্ঘ্যের।

২. এর তিনটি কোণও পরস্পর সমান, প্রতিটির পরিমাপ ৬০ ডিগ্রি।

৩. এর কোণগুলোর যোগ ১৮০ ডিগ্রি।

৪. এর তিনটি উচ্চতা ও পরস্পর সমান্তরাল এবং সমান দৈর্ঘ্যের।

৫. এর মধ্যরেখাগুলো ও পরস্পর সমান এবং ত্রিভুজের কেন্দ্র হতে সমান দূরত্বে অবস্থিত।

৬. এর ভিতরে অঙ্কিত বৃত্ত একেবারে সমবৃত্ত।

৭. এর প্রত্যেকটি বাহুর মধ্যে অঙ্কিত লম্বসম এবং কেন্দ্র হতে সমান দূরত্বে অবস্থিত।

৮. এর প্রতিটি কোণের বিপরীত বাহুও পরস্পর সমান।

৯. এর উপর ভিত্তি করে আরো অনেক সম্পর্ক প্রমাণ করা যায়।

সমবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র

যেহেতু সমবাহু ত্রিভুজের বাহু তিনটির দৈর্ঘ্য পরস্পর সমান। তাই বাহুভেদে সমবাহু ত্রিভুজ কে একটি সুষম ত্রিভুজ বলা হয়ে থাকে।

একারণে বিষমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র থেকে খুব সহজে সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র প্রতিপাদন করা যায়। বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a, b ও c একক হলে এবং সবগুলো বাহুর স্থলে a বসালে সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র প্রতিপাদিত হয়।

এছাড়াও, সমবাহু ত্রিভুজ একটি সুষম বহুভুজ ত্রিভুজ বলে আমরা জানি, যার প্রত্যেকটি কোণের পরিমাপ ৬০°।

এ কারণে সুষম বহুভুজের ক্ষেত্রফলের সূত্র থেকেও সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র সহজে নির্ণয় করা যায়।

মনেকরি, △ABC একটি সমবাহু ত্রিভুজ যার প্রত্যেকটি বাহুর দৈর্ঘ্য a একক এবং ক্ষেত্রফল A বর্গ একক। তাহলে সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র, A = √34 a2 বর্গ একক।

সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a একক এবং ক্ষেত্রফল A বর্গ একক হলে,
A = √34 a2 বর্গ একক।

ত্রিভুজ ক্ষেত্রের ভূমি এবং উচ্চতা মেপে এর ক্ষেত্রফল নির্ণয় করা যায়।

তাহলে আমরা সমবাহু ত্রিভুজের উচ্চতা বের করতে পারলে এর ক্ষেত্রফল নির্ণয় করতে পারব। সমবাহু ত্রিভুজের ক্ষেত্রফল হচ্ছে = √3a2/4 বর্গ একক।

ত্রিভুজ সংক্রান্ত আরো তথ্য হলো ত্রিভুজের একটি বাহুকে বর্ধিত করলে যে বৈশিষ্ট্য কোণ উৎপন্ন হয় তা এর বিপরীত অন্তঃস্থ কোণ দ্বয়ের সমষ্টির সমান হয়।

সমদ্বিবাহু ত্রিভুজ কাকে বলে, সমদিবাহু ত্রিভুজ কাকে বলে

কোন ত্রিভুজের দুইটি বাহুর দৈর্ঘ্য সমান হলে, তাকে সমদ্বিবাহু ত্রিভুজ বলে।

সমদ্বিবাহু ত্রিভুজের সমান দৈর্ঘ্যের বাহু দুইটির ছেদবিন্দুর বিপরীত বাহুকে তার ভূমি এবং ঐ ছেদবিন্দুতে উৎপন্ন কোণকে তার শিরঃকোণ বলা হয়।

চিত্রে <ABC-এ AB ও AC বাহুর দৈর্ঘ্য সমান, BC ভূমি এবং < A শিরঃকোণ।

সমদ্বিবাহু ত্রিভুজের বৈশিষ্ট্য

১. সমদ্বিবাহু ত্রিভুজে দুটি বাহু সমান হলেও তিনটি বাহু সমান নয়।

২. এর দুটি কোণ সমান হলেও তিনটি কোণ সমান নয়।

৩. সমান বাহু দুটির বিপরীত কোণ দুটি সমান হয়।

৪. একটি কোণ জেনে অপর দুটি কোণ বের করা যায়।

৫. এর উচ্চতাগুলো সমান্তরাল নয় এবং সমান লম্বর নয়।

৬. এর মধ্যরেখাগুলো সমান লম্বর নয় এবং কেন্দ্র থেকে সমান দূরত্বে নয়।

৭. এর ভিতরে অঙ্কিত বৃত্ত সমবৃত্ত নয়।

সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল

মনে করি, △ABC এ, ভুমি BC = b, AC = a এবং AB = a.

AD⊥BC আঁকি।

সমদ্বিবাহু ত্রিভুজের শীর্ষ থেকে ভূমির উপর লম্ব অঙ্কন করলে তা ভূমিকে সমদ্বিখণ্ডিত করে।

∴ BD = 12 BC

∴ BD = b2

সমকোণী △ABD হতে লিখা যায়,

AD² = AB² – BD²

বা, AD² = ‍a² – b²4

বা, AD² = 4a² – b²4

বা, AD = √4a² – b²√4

বা, AD = √4a² – b²2

∴ △ABC = 12 BC.AD

বা, △ABC = 12 b. √4a² – b²2

∴ △ABC = b4 √4a² – b²

সমদ্বিবাহু ত্রিভুজের ভুমি b একক, সমান সমান বাহুর দৈর্ঘ্য a একক এবং ক্ষেত্রফল A হলে
A = b4 √4a² – b² বর্গ একক।

বিষমবাহু ত্রিভুজ কাকে বলে

কোনো ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যই পরস্পর অসমান হলে, ত্রিভুজটিকে বিষমবাহু ত্রিভুজ বলা হয়।

চিত্রে, ABC ত্রিভুজটি একটি বিষমবাহু ত্রিভুজ, যার AB, BC ও CA বাহু তিনটি পরস্পর অসমান।

বিষমবাহু ত্রিভুজের বৈশিষ্ট্য

১. বিষমবাহু ত্রিভুজে তিনটি বাহুর মধ্যে একটি বাহু অপর দুটি বাহুর চেয়ে বড় বা ছোট হয়।

২. বড় বাহুর বিপরীত কোণটি ছোট বাহুর বিপরীত কোণের চেয়ে বড় হয়ে থাকে।

৩. ছোট বাহুর বিপরীত কোণটি বড় বাহুর বিপরীত কোণের চেয়ে ছোট হয়ে থাকে।

৪. এর মধ্যরেখাগুলো আলাদা আলাদা লম্বরের হয় এবং কেন্দ্র থেকে আলাদা দূরত্বে থাকে।

৫. এর উচ্চতাগুলো পরস্পর সমান্তরাল না-ও হতে পারে।

৬. এর ভিতরে অঙ্কিত বৃত্তগুলো একে অপরের সমান্তরাল না-ও হতে পারে।

৭. এটি একটি অসমবাহু ত্রিভুজ।

বিষমবাহু ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র, বিষমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র

বিষমবাহু ত্রিভুজ ক্ষেত্রফল = √{s(s -a)(s – b)(s – c)}  বর্গএকক   এখানে s = অর্ধপরিসীমা ( তিন বাহুর সমষ্টির অর্ধেক) a = ১ম বাহু b = ২য় বাহু c = ৩য় বাহু

বিষমবাহু ত্রিভুজের বাহু তিনটি পরস্পর অসমান। বিষমবাহু ত্রিভুজ অন্যান্য সকল ত্রিভুজকে প্রতিনিধিত্ব করে। তাই এই ত্রিভুজের ক্ষেত্রফলের সূত্র প্রয়োগ করে অন্যান্য সকল ত্রিভুজের ক্ষেত্রফল নির্ণয় করা যায়।

মনেকরি, ABC একটি বিষমবাহু ত্রিভুজ যার বাহু তিনটির দৈর্ঘ্য যথাক্রমে a একক, b একক, c একক; অর্ধ-পরিসীমা s একক এবং ক্ষেত্রফল A বর্গ একক। তাহলে, বিষমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্র,
A =√s(s – a)(s – b)(s – c) বর্গ একক; যেখানে s = a + b + c2.

বিষমবাহু ত্রিভুজের বাহুগুলোর দৈর্ঘ্য a একক, b একক, c একক; অর্ধ-পরিসীমা s একক এবং ক্ষেত্রফল A বর্গ একক হলে,

A =√s(s – a)(s – b)(s – c) বর্গ একক; যেখানে s = a + b + c2.

সূক্ষ্মকোণী ত্রিভুজ

কোনো ত্রিভুজের তিনটি কোণের প্রত্যেকটি সূক্ষ্মকোণ হলে, ত্রিভুজটিকে সূক্ষ্মকোণী ত্রিভুজ বলা হয়।

চিত্রে, ABC ত্রিভুজটি একটি সূক্ষ্মকোণী ত্রিভুজ। কারণ, <ABC, <BAC ও <ACB প্রত্যেক কোণই সূক্ষ্মকোণ। অর্থাৎ প্রত্যেকটি কোণের পরিমাপ 90° থেকে কম।

স্থূলকোণী ত্রিভুজ কাকে বলে

কোনো ত্রিভুজের একটি কোণ স্থূলকোণ হলে, ত্রিভুজটিকে স্থূলকোণী ত্রিভুজ বলা হয়।

চিত্রে, ABC ত্রিভুজটি একটি স্থূলকোণী ত্রিভুজ, যার <ABC স্থূলকোণ কিন্তু এর অন্য দুইটি কোণই সূক্ষ্মকোণ হবে। অর্থাৎ, <BAC ও <ACB উভয়ই সূক্ষ্মকোণ।

সমকোণী ত্রিভুজ কাকে বলে

কোনো ত্রিভুজের একটি কোণ সমকোণ হলে, ত্রিভুজটিকে সমকোণী ত্রিভুজ বলা হয়।

চিত্রে, ABC ত্রিভুজটি একটি সমকোণী ত্রিভুজ, যার <ABC সমকোণ। কিন্তু এর অন্য দুইটি কোণের প্রত্যেকটি সূক্ষ্মকোণ হবে। অর্থাৎ BAC ও BCA উভয়ই সুক্ষ্মকোণ।

সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে অতিভুজ ( Hypotenuse) বলে এবং সমকোণ সংলগ্ন বাহুর একটিকে ভূমি (Base) ও অপরটিকে উন্নতি বা উচ্চতা ( Altitude) ধরা হয়।

চিত্রে, ABC সমকোণী ত্রিভুজের AC বাহু অতিভুজ এবং BC বাহু ভূমি ও AB বাহু উচ্চতা।

সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র

সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয় করতে ত্রিভুজটির ভূমি ও লম্ব জানা থাকতে হয়। অর্থাৎ, সমকোণী ত্রিভুজের ভূমি ও লম্বের উপর উপর নির্ভর করে সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র নির্ণয় করা হয়। সমকোণী ত্রিভুজের একটি কোণ ৯০° বা সমকোণ হওয়ার কারণে ভূমি ও লম্ব পরস্পর লম্ব। সমকোণী ত্রিভূজের লম্ব ও ভূমির দৈর্ঘ্যের গুণফলকে অর্ধেক করলে ক্ষেত্রফল পাওয়া যায়।

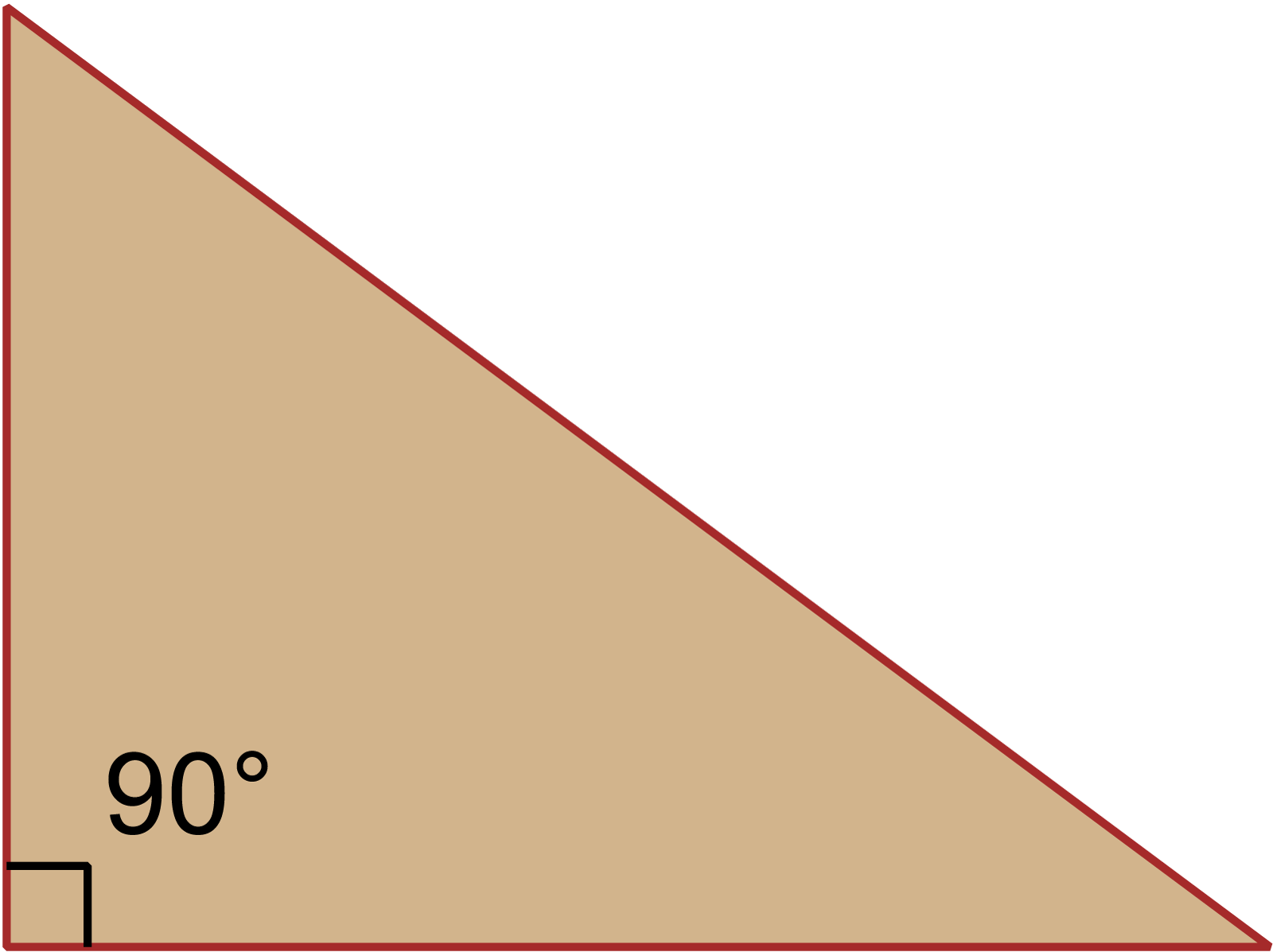
মনেকরি, △ABC একটি সমকোণী ত্রিভুজ যার লম্বের দৈর্ঘ্য a একক, ভূমির দৈর্ঘ্য b একক এবং ক্ষেত্রফল A বর্গ একক। তাহলে, সমকোণী ত্রিভুজের ক্ষেত্রফলের সূত্র,
A = 12 ab বর্গ একক।

সমকোণী ত্রিভুজের ভূমির দৈর্ঘ্য b একক, লম্বের দৈর্ঘ্য a একক এবং ক্ষেত্রফল A বর্গ একক হলে,
A = 12 ab বর্গ একক।

সমকোণী সমদ্বিবাহু ত্রিভুজ কাকে বলে

যে ত্রিভুজ একইসাথে সমদ্বিবাহু ও সমকোণী, তাই সমকোণী সমদ্বিবাহু ত্রিভুজ।অন্যভাবে বলা যায়, যে সমদ্বিবাহু ত্রিভুজের একটি কোণ ৯০ বা সমকোণ তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে।

আবার, কোন সমকোণী ত্রিভুজের দুইটি বাহু সমান হলে তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে।সুতরাং, যে ত্রিভুজের দুইটি বাহু সমান ও একটি কোণ সমকোণ তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে।সমকোণী সমদ্বিবাহু ত্রিভুজ এর সমকোণ ব্যতীত অন্য সূক্ষ্মকোণ দুইটি পরস্পর সমান। এই সূক্ষ্মকোণ দুইটির প্রত্যেকটির মান ৪৫।

ত্রিভুজের অন্তঃস্থ ও বহিঃস্থ কোণ

বহিঃস্থ কোণের সন্নিহিত কোণটি ছাড়া ত্রিভুজের অপর দুইটি কোণকে এই বহিঃস্থ কোণের বিপরীত অন্তঃস্থ কোণ বলে।

ত্রিভুজের একটি বাহুকে একদিকে বর্ধিত করলে সংশিষ্ট শীর্ষবিন্দুতে অন্তঃস্থ কোণের সন্নিহিত যে কোণটি উৎপন্ন হয়। তাকে ত্রিভুজের একটি বহিঃস্থ কোণ বলা হয়।

চিত্রে, ত্রিভুজ ABC এর BC বাহুকে D পর্যন্ত বর্ধিত করা হয়েছে।

<ACD ত্রিভুজটির একটি বহিঃস্থ কোণ। <ABC, <BAC ও <ACB ত্রিভুজটির তিনটি অন্তঃস্থ কোণ। বহিঃস্থ <ACD এর সন্নিহিত অন্তঃস্থ কোণ হচ্ছে <ACB এবং বিপরীত অন্তঃস্থ কোণ হচ্ছে <CBA ও <CAB।

ত্রিভুজের মধ্যমা, ত্রিভুজের মধ্যমা কাকে বলে

ত্রিভুজের কোন শীর্ষবিন্দু এবং এর বিপরীত বাহুর মধ্যবিন্দুর সংযোজক রেখাংশকে ত্রিভুজের একটি মধ্যমা বলা হয়। প্রত্যেক ত্রিভুজের তিনটি মধ্যমা আছে।

চিত্র ক-এ △ABC-এর শীর্ষবিন্দু এ এর বিপরীত বাহুর মধ্যবিন্দু D। অতএব সংজ্ঞানুসারে AD, △ABC-এর একটি মধ্যমা।

চিত্র খ-এ △ABC=~ △DEF এর মধ্যমাত্রয় হচ্ছে AD, BE ও CF। উলেখ্য ত্রিভুজের মধ্যমাত্রয় একটি এবং কেবলমাত্র একটি বিন্দুতে ছেদ করে।

ত্রিভুজের সর্বসমতা

একটি ত্রিভুজকে অপর একটি ত্রিভুজের উপর স্থাপন করলে যদি ত্রিভুজ দুইটি সর্বতোভাবে মিলে যায়, তবে ত্রিভুজ দুইটি সর্বসম হয়। সর্বসম ত্রিভূজের অনুরূপ বাহু ও অনুরূপ কোণগুলো সমান।

B চিত্রে, △ABC ও △DEF সর্বসম। কাজেই A.B.C শীর্ষগুলো যথাক্রমে D.E.F শীর্ষের উপর পতিত হলে, AB = DE, AC = DF, BC = EF হবে এবং <A = <D, <B = <E, <C = <F হবে।

দুইটি ত্রিভুজ △ABC ও △DEF সর্বসম বোঝাতে △ABC = △DEF লেখা হয়। আবার, দুইটি ত্রিভুজ সর্বসম হলে, এদের দ্বারা সীমাবদ্ধ ত্রিভুজক্ষেত্র দুইটিও সর্বসম হবে।

সূক্ষ্মকোণী ত্রিভুজ কাকে বলে, সূক্ষ্মকোণী ত্রিভুজ কাকে বলে চিত্র সহ, সূক্ষকোণী ত্রিভুজ কাকে বলে

যে ত্রিভুজের তিনটি কোণই সূক্ষ্মকোণ তাকে সূক্ষ্মকোণী ত্রিভুজ বলে।

সূক্ষ্মকোণী ত্রিভুজের যে কোন দুইটি কোণের সমষ্টি সবসময়ই ৯০^০ এর চেয়ে বেশি।

সূক্ষ্মকোণী ত্রিভুজের বাহুগুলো সমানও হতে পারে, আবার অসমানও হতে পারে।

সূক্ষ্মকোণী ত্রিভুজের শীর্ষত্রয় থেকে বিপরীত বাহুগুলোর উপর লম্ব অঙ্কণ করলে, লম্বত্রয়ের ছেদবিন্দু সবসময়ই ত্রিভুজের অভ্যন্তরে অবস্থিত।

কোণের ভিত্তিতে যে কয় ধরণের ত্রিভুজ আছে, তাদের মধ্যে একটি হলো সূক্ষ্মকোণী ত্রিভুজ।

সূক্ষ্মকোণী ত্রিভুজের ভরকেন্দ্র, অন্তকেন্দ্র, পরিকেন্দ্র ও লম্বকেন্দ্র সবই ত্রিভুজের অভ্যন্তরে অবস্থিত।

সূক্ষ্মকোণী ত্রিভুজ উদাহরণ

সূক্ষ্মকোণী ত্রিভুজের বৈশিষ্ট্য

সূক্ষ্মকোণী ত্রিভুজকে নিম্নলিখিত উপায়ে মোটামুটিভাবে আলাদা করা যায়।

• বিষমবাহু সূক্ষ্মকোণী ত্রিভুজ
• সমদ্বিবাহু সূক্ষ্মকোণী ত্রিভুজ
• সমবাহু সূক্ষ্মকোণী ত্রিভুজ

সূক্ষ্মকোণ বিশ্লেষণ করলে যেসব সূক্ষ্মকোণের বৈশিষ্ট্য পরিলক্ষিত হয়, তার একটি তালিকা করা যেতে পারে। নিচে সূক্ষ্মকোণ এর বৈশিষ্ট্য সমূহ তুলে ধরা হলো।

• সূক্ষ্মকোণের পরিমাপ ৯০^০ অপেক্ষা কম।
• একটি ত্রিভুজের সর্বোচ্চ তিনটি সূক্ষ্মকোণ থাকতে পারে।
• সূক্ষ্মকোণের পরিমাপ ০^০ অপেক্ষা বড় হয়।
• সূক্ষ্মকোণের পূরক কোণ একটি সূক্ষ্মকোণ হয়।
• সূক্ষ্মকোণের সম্পূরক কোণ একটি স্থূলকোণ হয়।
• সূক্ষ্মকোণের পরিপূরক কোণ একটি প্রবৃদ্ধ কোণ হয়।
• সূক্ষ্মকোণের বিপ্রতীপ কোণ একটি সূক্ষ্মকোণ হয়।
• সূক্ষ্মকোণের অনুরূপ কোণ একটি সূক্ষ্মকোণ হয়।
• সূক্ষ্মকোণের একান্তর কোণ একটি সূক্ষ্মকোণ হয়।
• যেকোনো একটি সূক্ষ্মকোণের সাথে সমকোণ যোগ করলে তা একটি স্থূলকোণ হয়।
• যেকোনো একটি সূক্ষ্মকোণের সাথে সরলকোণ যোগ করলে তা একটি প্রবৃদ্ধ কোণ হয়।
• যেকোনো একটি সূক্ষ্মকোণ, পূর্ণ কোণ থেকে বিয়োগ করলে বিয়োগফল একটি প্রবৃদ্ধ কোণ হয়।
• যেকোনো একটি সূক্ষ্মকোণ সবসময়ই একটি তির্যক কোণ।
• যেকোনো দুইটি সূক্ষ্মকোণের সমষ্টি সরলকোণ অপেক্ষা ক্ষুদ্রতর হয়।
• যেকোনো চারটি সূক্ষ্মকোণ যোগ করলে যোগফল পূর্ণকোণ অপেক্ষা ক্ষুদ্রতর হয়।
• কেবল দুইটি সূক্ষ্মকোণ বিশিষ্ট ত্রিভুজ হলো – হয় ত্রিভুজটি সমকোণী ত্রিভুজ অথবা স্থুলকোণী ত্রিভুজ।
• ত্রিভুজের সূক্ষ্মকোণের সংলগ্ন বাহু দুইটির যেকোনো একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয় তা একটি স্থূলকোণ।
• সকল সূক্ষ্মকোণী ত্রিভুজের যেকোনো দুইটি সূক্ষ্মকোণ যোগ করলে তা সবসময় এক সমকোণ বা ৯০^০ অপেক্ষা বড় হয়।
• সমকোণী ত্রিভুজের সূক্ষ্মকোণ দুইটির সমষ্টি এক সমকোণ বা ৯০^০।
• একটি স্থুলকোণী ত্রিভুজের সূক্ষ্মকোণ দুইটির সমষ্টি সবসময়ই ৯০^০ অপেক্ষা ছোট হয়।

স্থূলকোণী ত্রিভুজ কাকে বলে, স্থুলকোণী ত্রিভুজ কাকে বলে

যে ত্রিভুজের একটি কোণ স্থূলকোণ সেই ত্রিভূজকে স্থূলকোণী ত্রিভুজ বলে। স্থূলকোণী ত্রিভুজের স্থূলকোণ ব্যতীত এর অপর দুটি কোণ হচ্ছে সূক্ষ্মকোণ। স্থূলকোণী ত্রিভুজের তিনটি কোণের সমষ্টি ১৮০°।

যে কোণের মান ৯০ ° এর চেয়ে বড় এবং ১৮০ ° এর চেয়ে ছোট তাকে স্থূলকোণ বলে ।

স্থূলকোণী ত্রিভুজ যে ত্রিভুজের একটি কোণ স্থূলকোণ বা এক সমকোণ অপেক্ষা বড় তাকে স্থূলকোণী ত্রিভুজ বলে ।

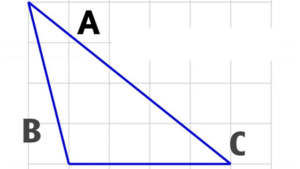
ABC একটি স্থূলকোণী ত্রিভুজ

স্থূলকোণী ত্রিভুজের বৈশিষ্ট্য

স্থূলকোণ এর বৈশিষ্ট্য স্থূলকোণী ত্রিভুজের ই অনুরূপ বৈশিষ্ট্য ——

1. স্থূলকোণী ত্রিভুজের একটি কোণ স্থূলকোণ অর্থাৎ ৯০ ° অপেক্ষা বেশি হয় কিন্তু ১৮০ ° অপেক্ষা কম

2. স্থূলকোণী ত্রিভুজের বাকী কোণ দুটি সূক্ষকোণ ।

সদৃশকোণী ত্রিভুজ কাকে বলে

একটি ত্রিভুজের তিনটি কোণ অপর একটি ত্রিভুজের তিনটি কোণ পরস্পর সমান হলে ত্রিভুজ দুইটিকে পরস্পর সদৃশকোণী ত্রিভুজ বলে। ত্রিভুজের তিন কোণের সমষ্টি ১৮০°। ফলে, একটি ত্রিভুজের দুইটি কোণ অপর একটি ত্রিভুজের দুইটি কোণ পরস্পর সমান হলে ত্রিভুজ দুইটির তৃতীয় কোণের পরিমাপও পরস্পর সমান হয়।

আরো অন্যান্য অতি জনপ্রিয় প্রশ্নোত্তর সম্পর্কে জানার জন্য এখানে ক্লিক করুন 

FAQ | ত্রিভুজ

আপনি কি চাকরি খুজঁছেন, নিয়মিত সরকারি ও বেসরকারি চাকরির সংবাদ পেতে ক্লিক করুন। বিভিন্ন সরকারি ও বেসরকারি ক্ষেত্রে মানব সম্পদ উন্নয়ন সংক্রান্ত প্রতিবেদন পাড়ার জন্য, ক্লিক করুন। হিন্দিতে শিক্ষামূলক ব্লগ পড়তে, এখানে ক্লিক করুন। এছাড়াও, স্বাস্থ, টেকনোলজি, বিসনেস নিউস, অর্থনীতি ও আরো অন্যান্য খবর জানার জন্য, ক্লিক করুন।