সামান্তরিক কাকে বলে

সামান্তরিক কাকে বলে

যে চতুর্ভূজের বিপরীত বাহুগুলো পরস্পর সমান্তরাল তাকে সামান্তরিক বলে। অন্যভাবে বললে, যে চতুর্ভুজের বিপরীত বাহুগুলো পরস্পর সমান ও সমান্তরাল কিন্তু কোণগুলো সমকোণ নয় তাকে সামান্তরিক বলে।

সংক্ষেপে সামান্তরিকের সংজ্ঞা হলো – চতুর্ভূজের বিপরীত বাহুগুলো পরস্পর সমান্তরাল হলে তাকে সামান্তরিক বলে।

সামান্তরিক হলো একটি বিশেষ ধরনের চতুর্ভুজ।

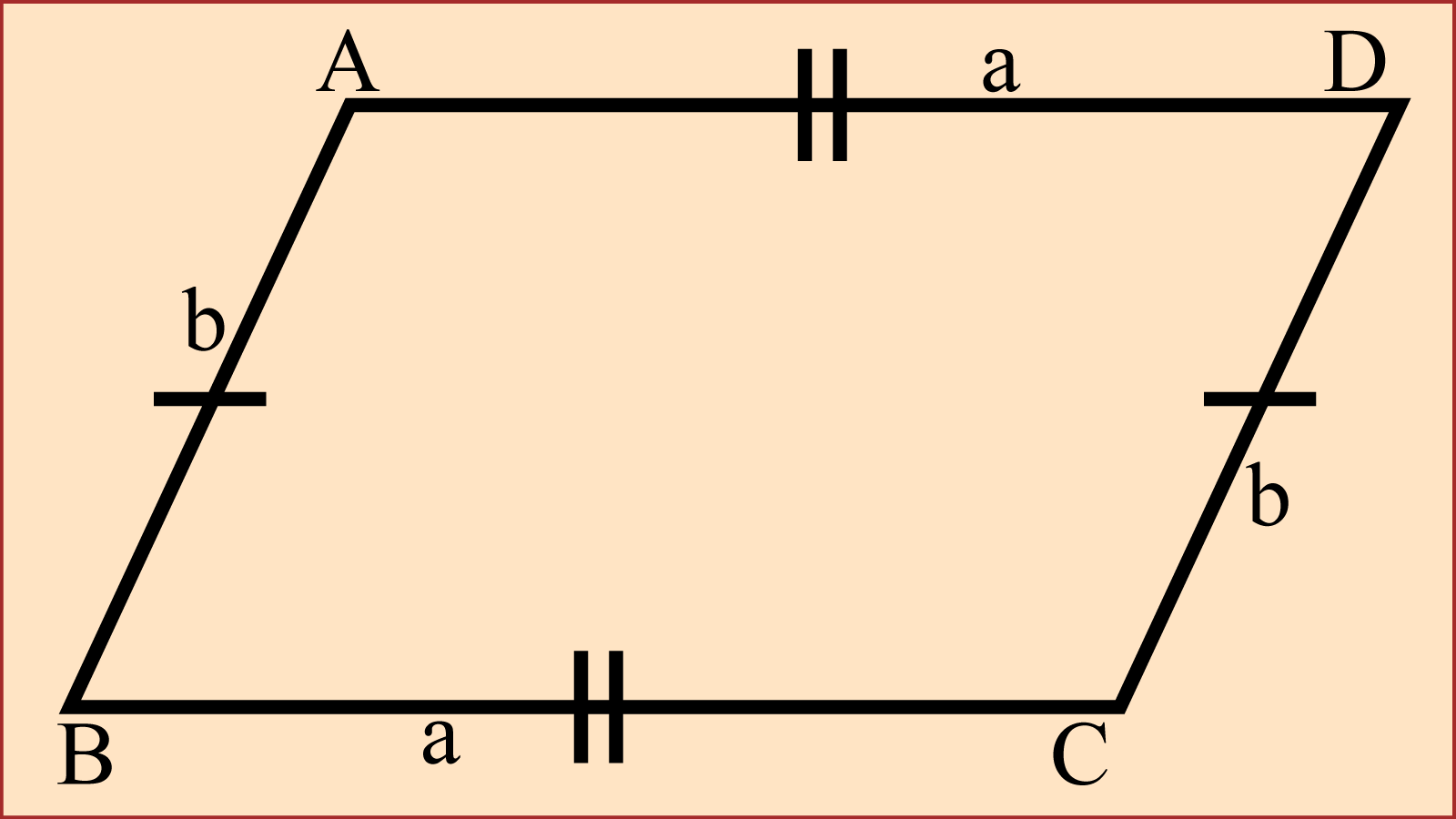
সামান্তরিকের বিপরীত বাহুগুলো পরস্পর সমান্তরাল। আবার, সামান্তরিকের বিপরীত বাহুগুলো পরস্পর সমান। সামান্তরিকের বিপরীত কোণগুলোও পরস্পর সমান।

আবার, সামান্তরিকের সন্নিহিত কোণ দুইটি পরস্পর সম্পূরক কোণ। অর্থাৎ, সামান্তরিকের যেকোনো সন্নিহিত কোণদ্বয়ের সমষ্টি দুই সমকোণ বা ১৮০°।

সামান্তরিকের কর্ণ দুইটি একে-অপরকে সমদ্বিখণ্ডিত করে।

সামান্তরিকের যেকোনো কর্ণ সামান্তরিকটিকে যে দুইটি ত্রিভুজে বিভক্ত করে তারা পরস্পর সর্বসম ত্রিভুজ।

সামান্তরিকের বৈশিষ্ট্য

• সামান্তরিকের বিপরীত বাহু দ্বয় পরস্পর সমান।
• সামান্তরিকের বিপরীত কোণ গুলো পরস্পর সমান।
• সামান্তরিকের যে কোন দুইটি সন্নিহিত কোণ পরস্পরের সম্পূরক।
• সামান্তরিকের কর্ণদ্বয় অসমান।
• সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে।
• সামান্তরিকের প্রত্যেক কর্ণ সামান্তরিককে দুইটি সর্বসম ত্রিভুজে বিভক্ত করে।
• সামান্তরিকের যেকোনো দুইটি সন্নিহিত কোণের সমষ্টি ১ সরলকোণ বা ১৮০ ডিগ্রি।
• সামান্তরিকের বাহুগুলোর উপর অঙ্কিত বর্গক্ষেত্রগুলোর সমষ্টি তার কর্ণদ্বয়ের উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের সমষ্টির সমান।

সামান্তরিকের সূত্র

সামান্তরিকের ক্ষেত্রফলঃ ( ভূমি × উচ্চতা) বর্গ একক

সামান্তরিকের পরিসীমাঃ ২( দৈর্ঘ্য + প্রস্থ) একক

সামান্তরিকের পরিসীমা

সামান্তরিকের সবগুলো বাহুর সমষ্টিকে সামান্তরিকের পরিসীমা বলে। একটি সামান্তরিকের সন্নিহিত যে কোন দুইটি বাহু জানা থাকলে সামান্তরিকের পরিসীমা নির্ণয় করা যায়।

সামান্তরিকের পরিসীমার সূত্র

মনে করি, একটি সামান্তরিকের সন্নিহিত বাহু দুইটি a এবং b.

আমরা জানি, সামান্তরিকের বিপরীত বাহুগুলো পরস্পর সমান।

সুতরাং, সামান্তরিকের পরিসীমা হবে-

P = (a+b+a+b) একক

বা, P = (২a+২b) একক

∴ P = ২(a+b) একক

সামান্তরিকের ক্ষেত্রফল

সামান্তরিকের ক্ষেত্রফল হলো একটি সামান্তরিক তার চারটি বাহু দ্বারা কতটুকু জায়গা বা সমতল দখল করে আছে তার সমান। সামান্তরিক ক্ষেত্রফল একাধিকভাবে নির্ণয় করা যায়। সামান্তরিকের ক্ষেত্রফল নির্ণয়ের আগে সামান্তরিকের ক্ষেত্রফলের সূত্র কি – তা জানা দরকার।

সামান্তরিকের ভূমিকে এর উচ্চতা দিয়ে গুণ করলে সামান্তরিকের ক্ষেত্রফল পাওয়া যায়।

সামান্তরিকের ক্ষেত্রফল এর সূত্র

সামান্তরিকের ক্ষেত্রফল নির্ণয় করতে গিয়ে প্রথমে জানতে হবে সামান্তরিকের ক্ষেত্রফল নির্ণয়ের সূত্র কি? তাহলে দেখা যাক, সামান্তরিকের ভূমি ও উচ্চতা দেওয়া থাকলে সূত্রটি কেমন হয়।

মনে করি, একটি সামান্তরিকের ভূমি b এবং উচ্চতা h.

সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক অর্থাৎ,

সামান্তরিকের ক্ষেত্রফল = (b × h) বর্গ একক

এখন, মনে প্রশ্ন জাগতে পারে যে, ভূমিকে উচ্চতা দিয়ে গুণ করলে সামান্তরিকের ক্ষেত্রফল পাওয়া যায়, কিভাবে? তাহলে আমরা সূত্রটি উদ্ভাবন করতে পারি।

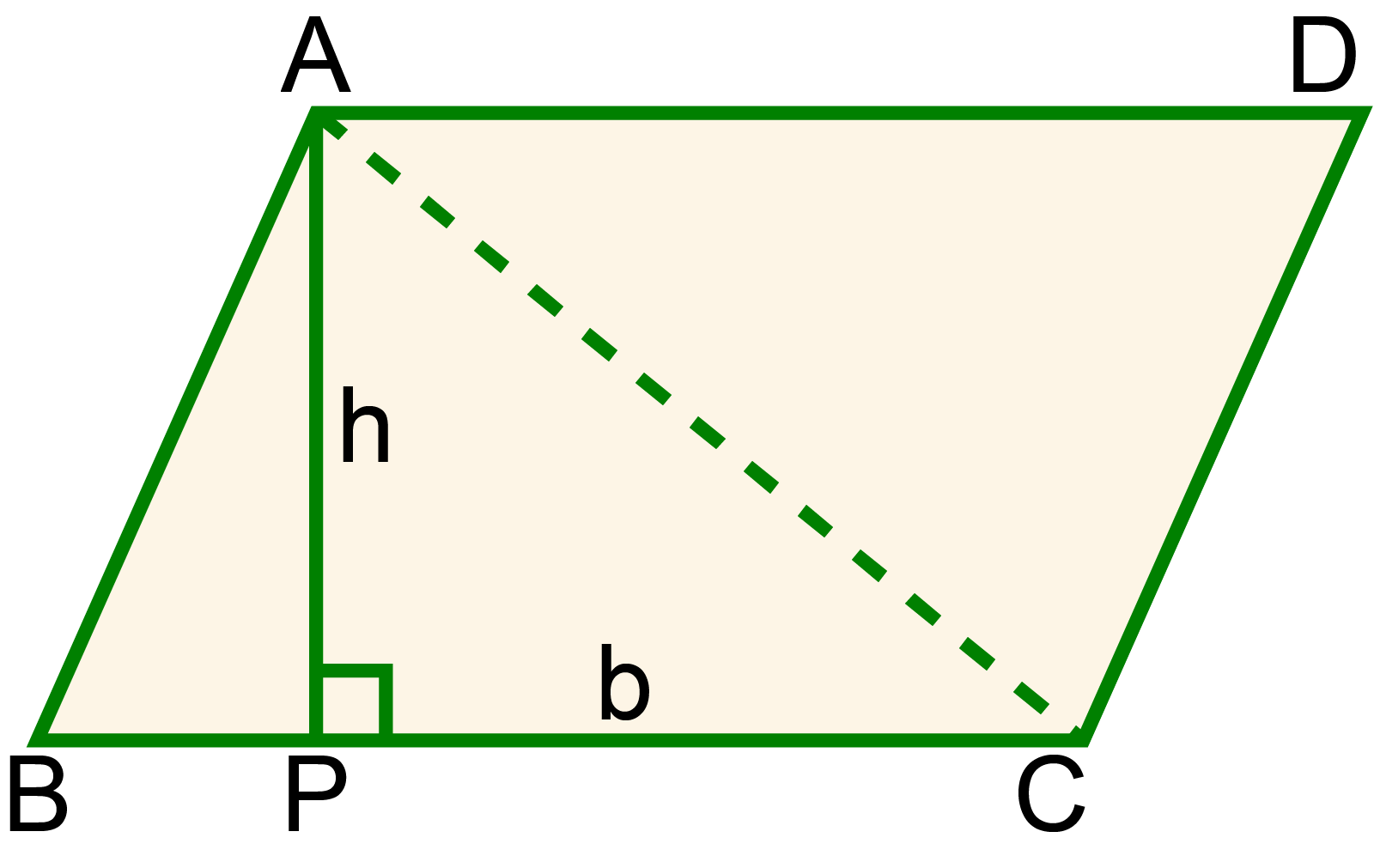
১ম ধাপঃ ABCD একটি সামান্তরিক আঁকি।

২য় ধাপঃ সামান্তরিকটির শীর্ষবিন্দু A থেকে ভূমির উপর একটি লম্ব AP আঁকি অর্থাৎ AP⊥BC আঁকি যেখানে AP = h এবং BC = b.

৩য় ধাপঃ AC কর্ণ আঁকি।

৪র্থ ধাপঃ আবার সামান্তরিকের কর্ণ সামান্তরিকটিকে দুইটি সর্বসম ত্রিভূজে বিভক্ত করে। ∴ ꕔABC = ꕔACD.

৫ম ধাপঃ ▱ABCD = △ABC + △ACD

বা, ▱ABCD = △ABC+△ABC [∵ △ABC = △ACD]

বা, ▱ABCD = ২.△ABC

বা, ▱ABCD = ২ × ১২ BC.AP

বা, ▱ABCD = BC.AP

∴ ▱ABCD= bh

∴ সামান্তরিকের ক্ষেত্রফল =( ভূমি × উচ্চতা ) বর্গ একক (প্রমাণিত)।

সামান্তরিক উদাহরণ

সামান্তরিকের কর্ণের সূত্র

সামান্তরিকের কর্ণ বলতে বুঝায় সামান্তরিকটির দুইটি বিপরীত কৌণিক বিন্দুর দুরত্ব। এই দুরত্ব নির্ণয় করতে হলে সামান্তরিকের কর্ণ নির্ণয়ের সূত্র কি তা আগে জানতে হবে।

মনে করি, একটি সামান্তরিকের সন্নিহিত বাহু দুইটি a ও b এবং তাদের অন্তর্ভূক্ত কোণ θ.

সুতরাং, সামান্তরিকের কর্ণ d = √(a² + b²- 2ab cosθ).

আরো অন্যান্য অতি জনপ্রিয় প্রশ্নোত্তর সম্পর্কে জানার জন্য এখানে ক্লিক করুন 

FAQ | সামান্তরিক

আপনি কি চাকরি খুজঁছেন, নিয়মিত সরকারি ও বেসরকারি চাকরির সংবাদ পেতে ক্লিক করুন। বিভিন্ন সরকারি ও বেসরকারি ক্ষেত্রে মানব সম্পদ উন্নয়ন সংক্রান্ত প্রতিবেদন পাড়ার জন্য, ক্লিক করুন। হিন্দিতে শিক্ষামূলক ব্লগ পড়তে, এখানে ক্লিক করুন। এছাড়াও, স্বাস্থ, টেকনোলজি, বিসনেস নিউস, অর্থনীতি ও আরো অন্যান্য খবর জানার জন্য, ক্লিক করুন।