- রম্বস কাকে বলে, রম্বস কাকে বলে ও বৈশিষ্ট্য, রম্বস কাকে বলে চিত্র সহ
- রম্বসের চিত্র
- রম্বস এর বৈশিষ্ট্য, রম্বসের বৈশিষ্ট্য, রম্বসের বৈশিষ্ট্য কি কি, রম্বসের ৫টি বৈশিষ্ট্য
- রম্বসের ক্ষেত্রফল
- রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র
- রম্বসের কর্ণ নির্ণয়ের সূত্র
- রম্বসের কর্ণ নির্ণয়ের সূত্র, রম্বসের কর্ণের সূত্র
- রম্বসের পরিসীমা
- রম্বসের পরিসীমার সূত্র
- রম্বসের বাহুর দৈর্ঘ্য নির্ণয়ের সূত্র
- রম্বস ও সামান্তরিকের পার্থক্য
- রম্বস ও বর্গক্ষেত্রের পার্থক্য, বর্গক্ষেত্র ও রম্বসের পার্থক্য
- বর্গ ও রম্বসের মধ্যে পার্থক্য
- FAQ | রম্বস
রম্বস কাকে বলে, রম্বস কাকে বলে ও বৈশিষ্ট্য, রম্বস কাকে বলে চিত্র সহ
যে চতুর্ভুজের সব বাহুর দৈর্ঘ্য সমান কিন্তু কোণ গুলো সমকোণ নয় তাকে রম্বস বলে।
যে চতুর্ভুজের চারটি বাহুর দৈর্ঘ্য পরস্পর সমান তাকে রম্বস বলে। অন্যভাবে বললে, যে চতুর্ভুজের সব বাহুর দৈর্ঘ্য সমান কিন্তু কোণগুলো সমকোণ নয় তাকে রম্বস বলে।
আরও কয়েকভাবে রম্বস এর সংজ্ঞা দেওয়া যায়। যেমন – সামান্তরিকের সন্নিহিত বাহুদ্বয় পরস্পর সমান হলে তাকে রম্বস বলে। রম্বস হলো বিশেষ ধরণের একটি চতুর্ভুজ যার বাহুগুলোর দৈর্ঘ্য পরস্পর সমান।
রম্বস হলো সামান্তরিকের একটি বিশেষ রূপ অর্থাৎ, সামান্তরিকের সন্নিহিত বাহুদ্বয় সমান হলে তখন তা রম্বস হয়ে যায়।
রম্বসের সবগুলো বাহু যেমন পরস্পর সমান; তেমনিভাবে রম্বসের বিপরীত কোণগুলো পরস্পর সমান। রম্বসের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে। আবার, রম্বসের কর্ণ দুইটি পরস্পরকে সমকোণে ছেদ করে।
যে চতুর্ভূজের বাহুগুলো পরস্পর সমান ও বিপরীত বাহুগুলো পরস্পর সমান্তরাল তাকে রম্বস বলে।নিম্নে রম্বসের চিত্র উপস্হাপন করা হলো।
রম্বসের চিত্র
রম্বসের বাহুগুলো সবগুলোই একে অপরের সমান কিন্তু এর কোণগুলোর মধ্যে দুইটি বিপরীত কোণ পরস্পর সমান।
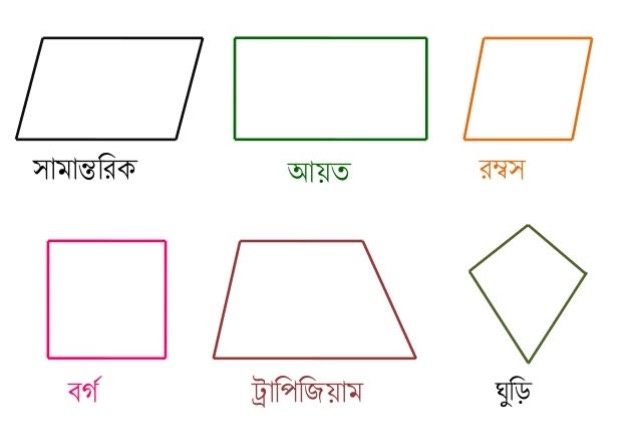
নিম্নে সামান্তরিক, আয়ত, রম্বস,বর্গ, ট্রাপিজিয়াম ও ঘুড়ি চতুর্ভূজক্ষেত্রের চিত্রগুলো দেওয়া হলো।
রম্বস এর বৈশিষ্ট্য, রম্বসের বৈশিষ্ট্য, রম্বসের বৈশিষ্ট্য কি কি, রম্বসের ৫টি বৈশিষ্ট্য
নিচে রম্বসের কয়েকটি বৈশিষ্ট্য উল্লেখ করা হলো।
- রম্বসের বিপরীত কোণ গুলো পরস্পর সমান।
- রম্বসের সকল বাহু সমান হয়।
- রম্বসের কর্ণদ্বয় অসমান অর্থাৎ সমান নয়।
- রম্বসের একটি কোন ও সমকোণ নয় ।
- রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে।
- কর্ণ 90° এ পরস্পরকে দ্বিখণ্ডিত করে।
- বিপরীত বাহুগুলি একটি রম্বসে সমান্তরাল।
- একটি রম্বসের বিপরীত কোণগুলি সমান।
- সন্নিহিত কোণগুলি 180° পর্যন্ত যোগ করে।
রম্বসের ক্ষেত্রফল
রম্বসের ক্ষেত্রফল বলতে বুঝায়, এর চারটি বাহু দ্বারা বেষ্টিত জায়গা। রম্বসের কর্ণদ্বয়ের মান জানা থাকলে এর ক্ষেত্রফল নির্ণয় করা যায়।
আবার, রম্বসের একটি বাহু ও সন্নিহিত কোণের পরিমাপ দেওয়া থাকলে এর কর্ণ নির্ণয় করা যায়; অতপর কর্ণদ্বয়ের মান ব্যবহার করে রম্বসের ক্ষেত্রফল নির্ণয় করা যায়। রম্বসের ক্ষেত্রফল একাধিক পদ্ধতিতে নির্ণয় করা যায়
রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র
রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র = 1/2 × কর্ণদ্বয়ের গুণফল
মনে করি, কোনো রম্বসের দুইটি কর্ণের দৈর্ঘ্য যথাক্রমে d1 ও d2. তাহলে
রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র = 1/2 × d1 × d2
প্রথম পদ্ধতিঃ রম্বসের কর্ণদ্বয়ের গুণফলকে অর্ধেক করলে ক্ষেত্রফল পাওয়া যায়।
ABCD রম্বসের কর্ণ দুইটি d1 ও d2 হলে, এর ক্ষেত্রফল হবে
A = 12 d1d2 বর্গ একক
দ্বিতীয় পদ্ধতিঃ সামান্তরিকের ভূমিকে উচ্চতা দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়। রম্বস একটি সামান্তরিক।
রম্বসের ভূমিকে উচ্চতা দ্বারা গুণ করলে ক্ষেত্রফল পাওয়া যায়।
রম্বসের কর্ণ নির্ণয়ের সূত্র
রম্বসের বিপরীত কৌণিক বিন্দু দুইটি যোগ করলে যে রেখাংশ পাওয়া যায় তাকে রম্বসের কর্ণ বলে।
রম্বসের এরূপ দুই জোড়া বিপরীত কৌণিক বিন্দু রয়েছে। দুই জোড়া কৌণিক বিন্দুর জন্য দুইট কর্ণ পাওয়া যায়। তাই রম্বসের কর্ণ দুইটি।
রম্বসের কর্ণ নির্ণয়ের সূত্র, রম্বসের কর্ণের সূত্র
রম্বসের বাহুর দৈর্ঘ্য জানা থাকলে রম্বসের কর্ণের দৈর্ঘ্য নির্ণয় করা যায়। তাহলে দেখা যাক- কিভাবে রম্বসের কর্ণ নির্ণয়ের সূত্র উদ্ভাবন করা যায়।
মনে করি, ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য AB, BC, CD ও AD; এবং AC ও BD এর দুইটি কর্ণ।
যেহেতু রম্বসের বাহুগুলো পরস্পর সমান, তাহলে মনে করি, AB = BC = CD = AD = a এবং কর্ণ AC = d1 ও BD = d2
রম্বসের পরিসীমা
রম্বসের বাহুগুলোর সমষ্টিকে রম্বসের পরিসীমা বলে।
যেহেতু রম্বসের বাহুগুলো পরস্পর সমান, তাই রম্বসের একটি বাহু জানা থাকলে এর পরিসীমা নির্ণয় করা যায়। আবার রম্বসের কর্ণ দুইটি জানা থাকলে সেখান থেকে এর বাহুর দৈর্ঘ্য নির্ণয় করা যায়; অতপর রম্বসের পরিসীমা নির্ণয় করা যায়।
রম্বসের পরিসীমার সূত্র
মনে করি, ABCD একটি রম্বস এবং AB = BC = CD = AD = a.
আমরা জানি, রম্বসের বাহুগুলো পরস্পর সমান।
সুতরাং, রম্বসের পরিসীমা P হলে,
P = (AB + BC + CD + AD) একক
বা, P = (a + a + a + a) একক
∴ P = 4a একক
রম্বসের বাহুর দৈর্ঘ্য নির্ণয়ের সূত্র
রম্বসের কর্ণদ্বয় জানা থাকলে অথবা রম্বসের ক্ষেত্রফল ও একটি কর্ণ দেওয়া থাকলে রম্বসের বাহুর দৈর্ঘ্য নির্ণয় করা যায়। তাহলে দেখা যাক, রম্বসের কর্ণ দুইট দেওয়া থাকলে কিভাবে রম্বসের বাহুর দৈর্ঘ্য নির্ণয়ের সূত্র উদ্ভাবন করা যায়।
প্রথম পদ্ধতিঃ মনে করি, ABCD রম্বসের বাহুগুলোর দৈর্ঘ্য a এবং কর্ণ দুইটি d1 ও d2 পরস্পর o বিন্দেুতে ছেদ করেছে। জানা আছে, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
রম্বসের বাহুর দৈর্ঘ্য নির্ণয়ের সূত্র =√{(১ম কর্ণ / 2)^2+( ২য় কর্ণ / 2)^2}
মনে করি, কোনো রম্বসের দুইটি কর্ণের দৈর্ঘ্য যথাক্রমে d1 ও d2. এবং রম্বসের বাহুর দৈর্ঘ্য a. তাহলে-
রম্বসের বাহুর দৈর্ঘ্য, a=√{(d1/2)^2+(d2/2)^2}
রম্বস ও সামান্তরিকের পার্থক্য
| রম্বস | সামন্তরিক |
|---|---|
| যে সামান্তরিকের দুইটি সন্নিহিত বাহু সমান, তাকে রম্বস বলে। | যে চতুর্ভুজের বিপরীত বাহুগুলো সমান ও সমান্তরাল কিন্তু কোনগুলো সমকোণ নয় তাকে সামান্তরিক বলে। |
| রম্বসের বিপরীত কোণ গুলো পরস্পর সমান। | সামান্তরিকের বিপরীত কোণগুলো সমান। |
| রম্বসের সকল বাহু সমান হয়। | সামান্তরিকের বিপরীত বাহুগুলো সমান্তরাল। |
| রম্বসের কর্ণদ্বয় অসমান অর্থাৎ সমান নয়। | সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে। |
| রম্বসের একটি কোনও সমকোণ নয়। | সামান্তরিকের বিপরীত কোণগুলো পরস্পর সমান। |
| রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে। | সামান্তরিকের কর্ণদ্বয় অসমান অর্থাৎ সমান নয়। |
রম্বস ও বর্গক্ষেত্রের পার্থক্য, বর্গক্ষেত্র ও রম্বসের পার্থক্য
| বর্গক্ষেত্র | রম্বস | |
| ১. | যে চতুর্ভুজের চারটি বাহু পরস্পর সমান ও সমান্তরাল এবং কোণগুলো প্রত্যেকটি সমকোণ, তাকে বর্গক্ষেত্র বলে। | রম্বস এমন একটি সামান্তরিক যার বাহুগুলো পরস্পর সমান এবং যার একটি কোণও সমকোণ নয়। |
| ২. | বর্গক্ষেত্রের প্রত্যেকটি কোণ সমকোণ। অর্থাৎ প্রত্যেক কোণের পরিমান ৯০ ডিগ্রি। | রম্বসের একটি কোণও সমকোণ নয়। |
| ৩. | বর্গক্ষেত্রের বাহুগুলো একে অপরের উপর লম্ব। | রম্বসের বাহুগুলো পরস্পরের উপর লম্ব নয়। |
| ৪. | বর্গক্ষেত্রের কর্ণদ্বয়ের দৈর্ঘ্য পরস্পর সমান। | রম্বসের কর্ণদ্বয়ের দৈর্ঘ্য পরস্পর সমান নয়। |
| ৫. | বর্গক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র = (১ বাহু)² | রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র = ½ X কর্ণদ্বয়ের গুণফল। |
| ৬. | বর্গক্ষেত্রের পরিসীমা সূত্র, s = 4a একক | রম্বসের পরিসীমা সূত্র, = 4 X (এক বাহু) একক |
| ৭. | বর্গক্ষেত্রের চিত্র | রম্বসের চিত্র |
বর্গ ও রম্বসের মধ্যে পার্থক্য
| বর্গ | রম্বস |
|---|---|
| বর্গের সকল কোন ৯০ ডিগ্রী। | রম্বসের বিপরীত কোনগুলো পরস্পর সমান। |
| বর্গের কর্ণদ্বয় সমান। | রম্বসের কর্ণদ্বয় অসমান। |
আরো অন্যান্য অতি জনপ্রিয় প্রশ্নোত্তর সম্পর্কে জানার জন্য এখানে ক্লিক করুন FAQ | রম্বস
Q1. রম্বসের প্রতিসাম্য রেখা কয়টি
Ans – রম্বসের প্রতিসাম্য রেখা হল 4 টি।
Q2. রম্বসের কর্ণ কয়টি
As – রম্বসের কর্ণ দুইটি।
Q3. রম্বসের ঘূর্ণন কোন কত
Ans – রম্বসের ঘূর্ণন কোণ 180 ডিগ্রি।
Q4. রম্বসের চার কোণের সমষ্টি কত
Ans – রম্বসের অভ্যন্তরীণ কোণের সমষ্টি 360 ডিগ্রি।
Q5. রম্বসের কর্ণদ্বয় কি সমান
Ans – রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
আপনি কি চাকরি খুজঁছেন, নিয়মিত সরকারি ও বেসরকারি চাকরির সংবাদ পেতে ক্লিক করুন। বিভিন্ন সরকারি ও বেসরকারি ক্ষেত্রে মানব সম্পদ উন্নয়ন সংক্রান্ত প্রতিবেদন পাড়ার জন্য, ক্লিক করুন। হিন্দিতে শিক্ষামূলক ব্লগ পড়তে, এখানে ক্লিক করুন। এছাড়াও, স্বাস্থ, টেকনোলজি, বিসনেস নিউস, অর্থনীতি ও আরো অন্যান্য খবর জানার জন্য, ক্লিক করুন। 



