- আলোর প্রতিফলন কাকে বলে
- আলোর প্রতিফলনের সূত্র
- আলোর প্রতিফলন কত প্রকার ও কি কি
- নিয়মিত প্রতিফলন কাকে বলে? উদাহরণ দাও?
- বিক্ষিপ্ত প্রতিফলন কাকে বলে? উদাহরণ দাও?
- নিয়মিত প্রতিফলন ও বিক্ষিপ্ত প্রতিফলনের পার্থক্য
- আলোর প্রতিফলনের চিত্র
- আলোর প্রতিফলনের নিয়ম
- আলোর প্রতিফলনের সূত্র ব্যাখ্যা | প্রতিফলনের সূত্র ব্যাখ্যা ও প্রমাণ
- গোলীয় দর্পণে আলোর প্রতিফলন
- FAQ | আলোর প্রতিফলন
আলোর প্রতিফলন কাকে বলে
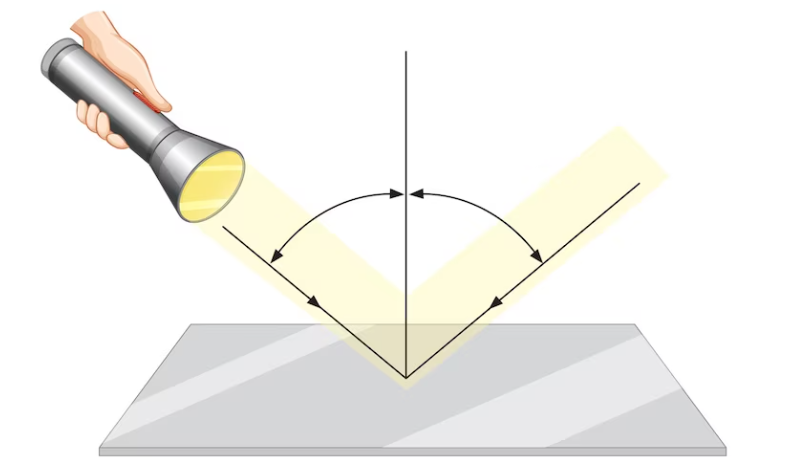
আলোর প্রতিফলন: আলোক রশ্মি যখন কোন স্বচ্ছ ও সমসত্ব মাধ্যম থেকে এসে অন্য এক মাধ্যমের বিভেদ তলে আপতিত হয়, তখন ওই আলোক রশ্মির কিছু অংশ দ্বিতীয় মাধ্যমের তল থেকে দিক পরিবর্তন করে আবার প্রথম মাধ্যমের ফিরে আসে, একে আলোর প্রতিফলন বলে।
প্রতিফলনের উদাহরণ: দিনের বেলা যখন সূর্য রশ্মি জলের মধ্যে পরে তখন ভালো করে খেয়াল করলে দেখা যে আলোক রশ্মি সামনের দেওয়ালে বা জলের পাশে গাছের মধ্যে আলোর ঝিকমিক করতে দেখা যায়। আসলে এটি আলোর প্রতিফলনের জন্য ঘটে।
সমসত্ত্ব মাধ্যমে আলো সরলরেখায় চলে। কিন্তু আলো যখন এক সমসত্ত্ব মাধ্যম থেকে অন্য এক সমসত্ত্ব মাধ্যমের তলে আপতিত হয়, তখন সাধারণত তিনটি ঘটনা ঘটে:
(1) আপতিত আলোর কিছু অংশ দ্বিতীয় মাধ্যম তল থেকে দিক পরিবর্তন করে পুনরায় প্রথম মাধ্যমে ফিরে আসে। আলোর এরূপ দিক পরিবর্তনকে প্রতিফলন বলে।
(2) আপতিত আলোর কিছু অংশ। দ্বিতীয় মাধ্যমে প্রবেশ করে অন্য পথে চলে যায়। একে আলোর প্রতিসরণ বলে।
(3) আপতিত আলোর অবশিষ্ট অংশ দ্বিতীয় মাধ্যম-তলে শোষিত হয়।
আলোর প্রতিফলনের সূত্র
- আপতিত রশ্মি, প্রতিফলিত রশ্মি এবং আপতন বিন্দুতে প্রতিফলকের ওপর অঙ্কিত অভিলম্ব একই সমতলে থাকে।
- আপতন কোন এবং প্রতিফলন কোণ পরস্পর সমান হয়।
.webp)
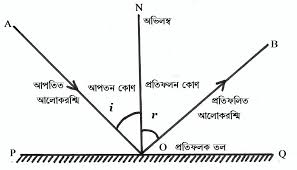
মনে করি, AO রশ্মি M1M2 দর্পণের O বিন্দুতে আপতিত হয়ে OC রশ্মিরূপে প্রতিফলিত হয়ছে। M1M2 দর্পণের O বিন্দুতে অঙ্কিত অভিলম্ব ON হলে প্রথম সুত্রানুসারে AO, OC এবং ON একই সমতলে থাকে এবং দ্বিতীয় সূত্রানুসারে, আপতন কোণ = প্রতিফলন কোণ বা <AON = <CON । অর্থাৎ, i = r
কোনো আলোক রশ্মি সমতল দর্পণে লম্বভাবে আপতিত হলে ঐ রশ্মির আপতন কোণ শূন্য হয়। ফলে ঐ রশ্মির প্রতিফলন কোণও শূন্য হয়। অর্থাৎ, প্রতিফলিত আলোকরশ্মি একই লম্বরেখা বরাবর প্রথম মাধ্যমে ফিরে যায়।
আলোর প্রতিফলন কত প্রকার ও কি কি
প্রতিফলকের (আয়না, স্থির জল, ঢেউ জল, মসৃণ ও অমসৃণ ধাতব তল, সাদা পর্দা, টিনের ঢেউ ইত্যাদির) প্রকৃতি অনুযায়ী প্রতিফলন দুই প্রকার। যথা –
- নিয়মিত প্রতিফলন
- বিক্ষিপ্ত প্রতিফলন
নিয়মিত প্রতিফলন কাকে বলে? উদাহরণ দাও?
নিয়মিত প্রতিফলন: আলোক রশ্মি গুচ্ছ কোনো মসৃণ সমতলে আপতিত হলে প্রতিফলিত আলোক রশ্মি গুলিও সমান্তরাল রশ্মি হিসেবে একটি নির্দিষ্ট দিকে চলে যায়। আলোক রশ্মির এই ধরনের প্রতিফলন কে নিয়মিত প্রতিফলন (বা Regular reflection) বলে।
নিয়মিত প্রতিফলনের উদাহরণ: আয়না, স্থির জল, মসৃণ ধাতব তল ইত্যাদি থেকে নিয়মিত প্রতিফলন হয়। এই প্রতিফলনের ফলে বস্তুর প্রতিবিম্ব গঠিত হয়। তাই সমতল দর্পণে বস্তুর প্রতিবিম্ব এবং পুকুরের স্থির জলে গাছের প্রতিবিম্ব দেখা যায়।
বিক্ষিপ্ত প্রতিফলন কাকে বলে? উদাহরণ দাও?
বিক্ষিপ্ত প্রতিফলন: আলোক রশ্মি গুচ্ছ কোনো অমসৃণ তলে আপতিত হলে প্রতিফলিত রশ্মি গুলি চারদিকে ছড়িয়ে পড়ে এবং আপতিত রশ্মি গুচ্ছের সঙ্গে প্রতিফলিত রশ্মি গুচ্ছের কোনো মিল থাকে না। এই ধরনের প্রতিফলনকে অনিয়মিত প্রতিফলন বা বিক্ষিপ্ত প্রতিফলন (Diffuse reflection) বলে।
বিক্ষিপ্ত প্রতিফলনের উদাহরণ: অমসৃণ ধাতব তল, ঢেউ টিনের উপর প্রতিফলন, সিনেমা হলের পর্দা, ঘষা কাঁচ, জলের ঢেউ ইত্যাদি।
নিয়মিত প্রতিফলন ও বিক্ষিপ্ত প্রতিফলনের পার্থক্য
| নিয়মিত প্রতিফলন | বিক্ষিপ্ত প্রতিফলন |
|---|---|
| নিয়মিত প্রতিফলন মসৃণ ও স্বচ্ছ প্রতিফলকে হয়। | বিক্ষিপ্ত প্রতিফলন অমসৃণ ও অস্বচ্ছ প্রতিফলকে হয়। |
| নিয়মিত প্রতিফলনে প্রতিফলক বস্তুর প্রতিবিম্ব গঠন করে। | বিক্ষিপ্ত প্রতিফলনে বস্তুর প্রতিবিম্ব পাওয়া যায় না। |
| নিয়মিত প্রতিফলনে প্রতিফলককে ঘুরিয়ে প্রতিফলিত রশ্মির দিক পরিবর্তন করা যায়। | বিক্ষিপ্ত প্রতিফলনের ক্ষেত্রে প্রতিফলককে ঘুরিয়ে প্রতিফলিত রশ্মিকে ইচ্ছা মতো নির্দিষ্ট কোনো দিকে ফেলা যায় না। |
| নিয়মিত প্রতিফলনে প্রতিফলিত আলো একটি নির্দিষ্ট দিক থেকে বেশি পরিমাণে আমাদের চোখে এসে পরে। ফলে, কেবল মাত্র সেই দিক থেকে তাকালেই প্রতিফলক চকচকে দেখায়। | বিক্ষিপ্ত প্রতিফলনে প্রতিফলিত রশ্মি গুলি চারদিকে ছড়িয়ে পড়ায় অল্প অথচ সমপরিমাণ আলো আমাদের চোখে পৌঁছায় এবং যে কোনো দিক থেকেই প্রতিফলক তালটিকে সমান উজ্জ্বল দেখায়। |
| নিয়মিত প্রতিফলনে প্রতিফলিত রশ্মি গুচ্ছ আপতিত রশ্মি গুচ্ছের অনুরূপ হয়। | বিক্ষিপ্ত প্রতিফলনে আপতিত ও প্রতিফলিত রশ্মি গুচ্ছের মধ্যে কোনো সাদৃশ্য থাকে না। |
আরো পড়তে : রশ্মি কাকে বলে, আপতিত রশ্মি কাকে বলে, প্রতিসরিত রশ্মি কাকে বলে
আলোর প্রতিফলনের চিত্র
আলোর প্রতিফলনের নিয়ম
আলোর প্রতিফলনের ১ম সূত্র: আপতিত রশ্মি প্রতিফলিত রশ্মি এবং অপদান বিন্দুতে প্রতিফলকের উপর অঙ্কিত অবিলম্ব একই সমতলে থাকে।
আলোর প্রতিফলনের ২য় সূত্র: আপতান কোণ এবং প্রতিফলন কোণ পরস্পর সমান হয়।
আলোর প্রতিফলনের সূত্র ব্যাখ্যা | প্রতিফলনের সূত্র ব্যাখ্যা ও প্রমাণ
উপকরণ: একটি সমতল দর্পণ, একটি ড্রয়িং বোর্ড, চারটি বড়ো পিন, চারটি বোর্ডপিন, স্কেল, চাঁদা, সরু পেনসিল এবং একখানা পরিষ্কার সাদা কাগজ।
আলোর প্রতিফলনের সূত্র ব্যাখ্যা ও প্রমাণ: প্রথমে ড্রয়িং বোর্ডের ওপর সাদা কাগজ পাতা হল। তারপর কাগজের চার কোণায় চারটি বোর্ডপিন পুঁতে কাগজটিকে টানটান করে আটকানো হল।
কাগজের ওপর স্কেল ও পেন্সিলের সাহায্যে একটি রেখা MM’ টানা হল। ওই রেখা বরাবর সমতল দর্পণটিকে খাড়াভাবে রাখা হল।
দর্পণের সামনে দুটি পিন A ও B -কে কাগজের ওপর লম্বভাবে একই রেখায় এমনভাবে পোঁতা হল যাতে AB রেখা MM’ রেখার সঙ্গে তির্যকভাবে থাকে।
এই অবস্থায় কাগজের তল বরাবর একটি চোখ রেখে আরও দুটি পিন C ও D-কে এমনভাবে পোঁতা হল যাতে পিন দুটি A ও B-এর প্রতিবিম্বের সঙ্গে একই সরলরেখায় থাকে।
এরপর কাগজের ওপর থেকে দর্পণ ও পিনগুলিকে উঠিয়ে নেওয়া হল। A, B এবং C, D বিন্দুগুলি যুক্ত করে দর্পণের দিকে বাড়ানো হল এবং তারা MM’ রেখাকে O বিন্দুতে ছেদ করল। সবশেষে O বিন্দুতে দর্পণের অবস্থানের ওপর ON লম্ব টানা হল। তাহলে AB হল আপতিত রশ্মি, CD হল প্রতিফলিত রশ্মি, ON হল আপতন বিন্দুতে অঙ্কিত অভিলম্ব।
A, B, O, C, D এবং N – এই বিন্দুগুলি কাগজের তলের ওপর থাকায় বলা যায় যে আপতিত রশ্মি, প্রতিফলিত রশ্মি এবং আপতন বিন্দুতে অঙ্কিত অভিলম্ব একই সমতলে আছে। সুতরাং প্রতিফলনের প্রথম সূত্রের সত্যতা প্রমাণিত হল।
চাঁদার সাহায্যে ∠AON ও ∠BON মেপে দেখা গেল ∠AON = ∠DON হয়েছে। এবারে A ও B পিন দুটির অবস্থান পরিবর্তিত করে পরীক্ষাটি আরও দু-বার করা হল। দেখা গেল প্রতি ক্ষেত্রেই আপতন কোণ ও প্রতিফলন কোণের মান পরস্পর সমান হয়েছে। সুতরাং প্রতিফলনের দ্বিতীয় সূত্রটি প্রমাণিত হল।
গোলীয় দর্পণে আলোর প্রতিফলন
গোলিও দর্পণে আলো কিভাবে প্রতিফলিত হয় সে সম্পর্কে বুঝতে চাইলে আমাদেরকে সমতল দর্পণ সম্পর্কে খুব ভালো ভাবে জানতে হবে। তাই চলো আগে আমরা সমতল দর্পণে আলোর প্রতিফলনের সূত্র গুলো একটু মনে করে নিই। এগুলো তোমরা এর আগের শ্রেণীতে পড়েছো তাই আশা করছি তোমাদের অল্প বিস্তর মনেও থাকবে। তোমরা সেখানে থেকে জানো যে আলোর প্রতিফলন প্রধানত দুটো সূত্র মেনে চলে। এই সূত্র দুটো হলো –
- আপতিত আলোক রশ্মি, প্রতিফলিত আলোক রশ্মি ও আপতন বিন্দুতে প্রতিফলকের (Mirror) ওপর অঙ্কিত অভিলম্ব একই সমতলে অবস্থান করে।
- আপতন কোণ (Incident Angle) সবসময় প্রতিফলন কোণের (Reflection Angle) সমান হয়।
তো এখানে মনে রাখবে গোলিও দর্পনে আলোর প্রতিফলনও এই সূত্র দুটোই মেনে চলে। এখানে তোমাদের মনে হয়তো একটা প্রশ্ন আসতে পারে যে এই সূত্র দুটো তো সমতল দর্পনের ক্ষেত্রে প্রযোজ্য কারণ সেটি সমতল হয় কিন্তু এখানে আমরা যে গোলিও দর্পণ নিয়ে আলোচনা করতে যাচ্ছি সেটির তল বা surface তো গোলিও হয়। তাহলে এই গোলিও তলের ওপর এই একই নিয়ম গুলো কিভাবে প্রযোজ্য হবে। এটা বোঝার জন্য আমাদের জানতে হবে যে গোলিও দর্পণের তল বা Surface টি আসলে কিভাবে গঠিত হয়। যদি তোমরা গোলিও দর্পণের খুব ক্ষুদ্র একটি অংশকে zoom করে দ্যাখো তাহলে বুঝতে পারবে যে এটি আসলে খুব ছোটো ছোটো সমতল দর্পণের অংশ নিয়ে গঠিত।
যেমনটা এখানে আমরা দেখতে পাচ্ছি। এখানে এই ক্ষুদ্র অংশটির ওপর যখন আরো ক্ষুদ্র একটি ক্ষুদ্র বিন্দুতে আলোক রশ্মিটি পড়ে তখন আলোটি সমতল দর্পণের নিয়ম মেনেই প্রতিফলিত হয়। কারণ আমরা এখানে যেহেতু সম্পূর্ণ দর্পনটিকে একসাথে দেখতে পাচ্ছি তাই বুঝতে পারছি যে এটি একটি গোলিও দর্পণ কিন্তু এই আপতিত আলোটি তো শুধু একটি ছোট্ট বিন্দুতে আপতিত হচ্ছে আর সেটি কেবল মাত্র ওই বিন্দুটিকেই দেখতে পাচ্ছে। এই বিন্দুটির আসে পাশে কি আছে সে সব সম্পর্কে আলোটি কিন্তু জানে না। তাই উত্তল দর্পনের ক্ষেত্রেও আলো সমতল দর্পণে প্রযোজ্য আলোর প্রতিফলনের সূত্র দুটোই মেনে চলে। এখন এই বিন্দুটিতে যদি একটা অভিলম্ব অঙ্কন করা হয়, তাহলে প্রতিফলনের প্রথম সূত্র অনুসারে আমরা দেখতে পাবো যে আপতিত রশ্মি, প্রতিফলিত রশ্মি আর আপতন বিন্দুতে অঙ্কিত অভিলম্ব একই সমতলে অবস্থান করবে। আর দ্বিতীয় সূত্র অনুসারে আপতন কোন <i প্রতিফলন কোন <r এর সমান হবে।
এখন এটি একটি অবতল দর্পনের ক্ষেত্রে কিভাবে পাওয়া যাবে? তাহলে চলো একটি অবতল দর্পণ নেয়া যাক। মনে করো দর্পনটির ওপর এই বিন্দুটিতে একটি আলোক রশ্মি আপতিত হলো। এখন এই আলোটি প্রতিফলনের সূত্র মেনেছে কিনা সেটি দেখার জন্য এই বিন্দুটিতে একটি অভিলম্ব অঙ্কন করতে হবে। অভিলম্বটি আকার জন্য প্রথমে এই বিন্দুটিতে একটি স্পর্শক অঙ্কন করতে হবে। আর স্পর্শকটি আমরা কিভাবে পাবো ? আমরা এর আগেই দেখেছি যে গোলিও দর্পণ গুলো হলো একটি গোলকের অংশ। আর গোলক বা বৃত্তের কোনো বিন্দুতে স্পর্শক অঙ্কন করা আমরা জ্যামিতিতে শিখেছি। এর জন্য বৃত্তের কেন্দ্র আর ওই বিন্দুটিকে যোগ করে বৃত্তের ব্যাসার্ধটি পাওয়া যাবে। তারপর এই বিন্দুটিতে ব্যাসার্ধের সাথে সমকোনে একটি রেখা আঁকতে হবে।
এই রেখাটি হলো এই বিন্দুতে অঙ্কিত স্পর্শক। তাহলে অভিলম্বটি এই স্পর্শকের সাথে 90° কোন তৈরি করে। এখানে তোমরা ভালো করে লক্ষ করে দেখো যে স্পর্শকের ওপর অঙ্কিত অভিলম্বটি হলো actually এই বৃত্তটির ব্যাসার্ধ । অবশ্য বৃত্তটি এখানে একটি গোলককে represent করছে। এখান থেকে আমরা বুঝতে পারলাম যে দর্পনের ওপর অবস্থিত যে কোনো বিন্দুতে অভিলম্ব অঙ্কন করার জন্য ওই বিন্দুটিকে বক্রতা কেন্দ্রের সাথে যোগ করে দিলেই আমরা অভিলম্বটি পেয়ে যাবো। এবং এটি উত্তল ও অবতল যে কোনো গোলিও দর্পনের ক্ষেত্রেই একই রকম ভাবে প্রযোজ্য হয়। তাহলে এখানে আপতন কোণের মান i হলে প্রতিফলন কোণের মানও এর সমান হবে। এছাড়াও এখানে রশ্মি দুটো এবং অভিলম্ব একই সমতলে অবস্থান করছে। তাহলে এখান থেকে আমরা বুঝতে পারলাম যে গোলিও দর্পণের ক্ষত্রেও আলো প্রতিফলনের সূত্র দুটো মেনে চলে।
আরো অন্যান্য অতি জনপ্রিয় প্রশ্নোত্তর সম্পর্কে জানার জন্য এখানে ক্লিক করুন FAQ | আলোর প্রতিফলন
Q1. আলোর প্রতিফলন কি
Ans – আলো কোনো স্বচ্ছ মাধ্যমের ভিতর দিয়ে যাওয়ার সময় অন্য কোন মাধ্যমে বাধা পেলে দুই মাধ্যমের বিভেদতল থেকে কিছু পরিমাণ আলোক রশ্মি আগের মাধ্যমে ফিরে আসে, এ ঘটনাকে আলোর প্রতিফলন বলে। অথবা আলোক উৎস থেকে আপতিত রশ্মি কোন তলে বা পৃষ্ঠে বাধা পেলে কিছু আলো পুনরায় আগের মাধ্যমে ফিরে আসে, এ ঘটনাকে আলোর প্রতিফলন বলে।
Q2. আলোর প্রতিফলনের সূত্র কয়টি, আলোর প্রতিফলনের দুটি সূত্র
Ans – আলোর প্রতিফলনের সূত্র দুটি। প্রথম সূত্র : আপতিত রশ্মি, প্রতিফলিত রশ্মি এবং আপাতন বিন্দুতে প্রতিফলকের উপর অঙ্কিত অভিলম্ব একই সমতলে অবস্থান করে। দ্বিতীয় সূত্র : প্রতিফলন কোণ , আপতন কোণের সমান হয়।
Q3. কোন বর্ণের আলোর প্রতিফলন সবচেয়ে বেশি
Ans – লাল বর্নের আলোর প্রতিফলন বেশী।
Q4. আলোর প্রতিফলনের সূত্র কে আবিষ্কার করেন
Ans – ১৬২০ সালে হল্যান্ডের বিজ্ঞানী স্নেল (Willebrord Snellius) সর্বপ্রথম আলোর প্রতিফলনের সূত্র আবিষ্কার করেন।
আপনি কি চাকরি খুজঁছেন, নিয়মিত সরকারি ও বেসরকারি চাকরির সংবাদ পেতে ক্লিক করুন। বিভিন্ন সরকারি ও বেসরকারি ক্ষেত্রে মানব সম্পদ উন্নয়ন সংক্রান্ত প্রতিবেদন পাড়ার জন্য, ক্লিক করুন। হিন্দিতে শিক্ষামূলক ব্লগ পড়তে, এখানে ক্লিক করুন। এছাড়াও, স্বাস্থ, টেকনোলজি, বিসনেস নিউস, অর্থনীতি ও আরো অন্যান্য খবর জানার জন্য, ক্লিক করুন।